[해외 DS] 기원전 5세기 학자는 어떻게 무리수를 발견했을까
무리수 발견을 둘러싼 수많은 미신과 이야기
직각 이등변 삼각형과 피타고라스 정리를 이용하여 무리수 존재 증명
무리수 발견은 그 당시 사람들에게 엄청난 충격을 줘
[해외DS]는 해외 유수의 데이터 사이언스 전문지들에서 전하는 업계 전문가들의 의견을 담았습니다. 글로벌AI협회(GIAI)에서 번역본에 대해 콘텐츠 제휴가 진행 중입니다.

기원전 5세기 학자인 히파소스는 무리수를 발견한 죄로 사형당했다는 전설이 내려오고 있다. 하지만 전문가들은 기원전 5세기에 실제로 무슨 일이 일어났는지 확신할 수 없다는 의견이다. 이에 관해서는 수많은 미신이 있으며 어떤 미신과 이야기가 진실인지는 아직 밝혀지지 않았다고 한다.
세상이 유리수와 무리수로 이루어졌다고 믿었던 피타고라스 학파
피타고라스 학파는 수학을 연구하며 자연수와 유리수로 세상을 표현할 수 있다고 믿었다. 그러나 피타고라스 학파의 일원인 히파소스는 오각형의 길이 비율을 조사하던 중 한 변의 길이가 분수로 표현할 수 없다는 사실을 발견하고 자연수와 유리수 외에 다른 수가 존재함을 깨닫는다.
그러나 여기서부터 히파소스에 대한 이야기는 다양하다. 한 이야기에 따르면, 히파소스가 피타고라스 학파 주장에 반하는 결과를 발견하여 이에 피타고라스 학파는 불쾌감을 느꼈으며 히파소스가 무리수를 발견했다는 사실을 공개하여 피타고라스 학파의 규칙을 위반했다고 전해진다. 어느 것이 진실이든 히파소스는 무리수를 발견한 후 바다에 빠져 익사했다. 이에 대해서도 여러 이야기가 있다. 일부는 피타고라스 학파 일원이 히파소스를 배 밖으로 던졌다고 하며 다른 이들은 그의 죽음이 피타고라스 학파가 내린 신의 형벌이라고 한다.
피타고라스 학파를 둘러싼 미신
전문가들이 히파소스에 관한 이야기를 역사적 증거와 비교해 본 결과, 이야기는 순수한 전설일 가능성이 높다고 한다. 히파소스가 무리수를 발견한 것이 사실이면, 히파소스의 발견은 오히려 피타고라스 학파가 자랑스러워할 만한 업적으로 칭송받았을 것이다. 실제로 피타고라스 학파는 철학적, 정치적으로 박해를 받았으며 학파에 대한 부정적인 이야기를 꾸며냈을 가능성이 있다.
피타고라스 학파에 대해 알려진 사실은 별로 없다. 피타고라스는 수학 외에도 다양한 분야에 관심을 가져 고대 그리스인들과 차별화되는 견해를 제시했다. 피타고라스 학파는 부를 거부하고 채식 위주의 금욕적인 생활을 했으며 환생을 믿는 등 고대 그리스인들과 다른 행동을 보였다. 이단으로 여겨진 피타고라스 학파는 여러 차례 공격을 받았으며, 피타고라스가 사망한 후 학파는 역사 속으로 사라졌다.
히파소스는 어떻게 무리수를 증명했을까
논란의 중심인 무리수 증명에 대해 알아보자. 무리수는 두 정수의 비율로 나타낼 수 없는 실수를 말한다. 히파소스는 직각 이등변 삼각형을 이용해 무리수가 존재함을 보였다. 밑에 사진처럼 두 변의 길이가 $a$이고 빗변의 길이가 $c$인 직각 이등변 삼각형을 증명에 활용했다.
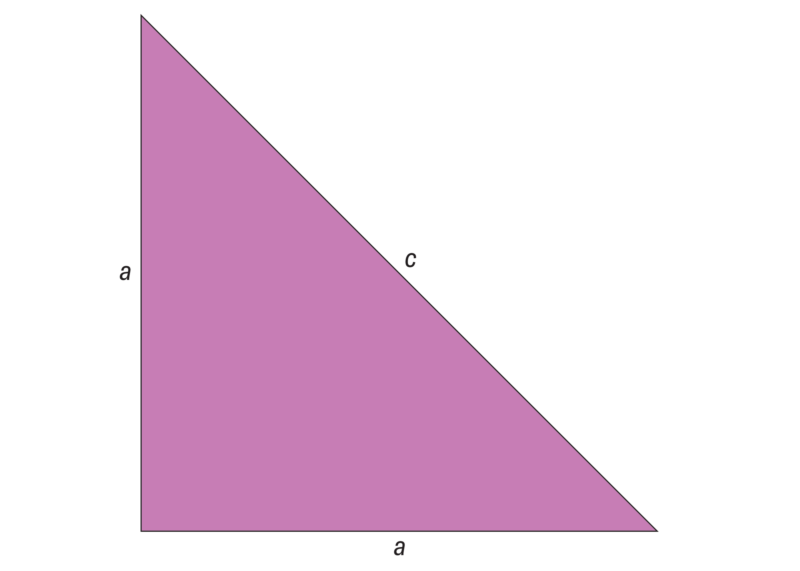
삼각형의 밑변과 빗변의 비율은 $\frac{a}{c}$다. 피타고라스 학파가 주장했듯이 자연수와 유리수만 존재한다면, $a$와 $c$에 대해 서로소인 가장 작은 자연수를 고를 수 있다. 예를 들어 비율이 $\frac{2}{3}$라면 $a=2$, $c=3$이 된다.
히파소스는 피타고라스 학파가 주장한 것에 모순이 있음을 보여 무리수의 존재성을 증명했다. 먼저 히파소스는 피타고라스 정리($a^2 + b^2 = c^2$)를 사용하여 빗변의 길이 $c$를 $a$에 대한 함수로 표현했다($2a^2=c^2$). $a$와 $c$가 자연수이므로 $c^2$은 짝수인 것을 알 수 있다. 따라서 $c$를 다르게 표현하면, $c=2n$으로 나타낼 수 있고 여기서 $n$은 자연수다.
$c = 2n$을 원래 방정식에 대입하면 $2a^2 = (2n)^2 = 4n^2$이 된다. 2를 양변에 나누면 $a^2 = 2n^2$이 되고 $a$는 짝수라는 것을 알 수 있다. 그러면 처음에 가정했던 $a$와 $c$가 서로소라는 가정에 모순이 생기고 $\frac{a}{c}$라는 무리수가 존재한다.
시대를 앞서간 발견
히파소스는 피타고라스 학파의 주장에 모순을 보여 직각 이등변 삼각형의 $\frac{a}{c}$ 비율이 유리수가 될 수 없다는 결론을 내렸다. 다시 말해 두 정수의 비율로 표현할 수 없는 숫자가 존재한다는 것이다. 예를 들어 직각 이등변 삼각형에서 $a = 1$이면 $c = \sqrt{2}$가 된다. 오늘날에는 $\sqrt{2}$가 무리수라는 사실이 잘 알려져 있다.
수학과 과학이 발전한 현재에서 볼 때 무리수의 존재는 놀랍지 않다. 그러나 약 2500년 전에는 이러한 깨달음이 사람들에게 상당한 충격을 줬을 것으로 예상한다. 또한 무리수의 발견은 수학 세계관을 뒤집어 놓았을 것으로 추측된다. 따라서 무리수 발견에 수많은 신화와 전설이 있는 것도 당연한 일이다.
*편집진: 영어 원문의 출처는 사이언티픽 아메리칸(Scientific American)으로 본지의 편집 방향과 일치하지 않을 수도 있습니다.