[해외 DS] 반세기 만에 찾은 ‘아인슈타인 타일’ ②, 아마추어 수학자의 샘솟는 아이디어

모자의 평면 타일링 가능성, 재귀적 계층 확장으로 설명
'메타타일'의 분해·조합으로 완전한 비주기성도 증명해
'유령' 타일마저 발견, "반사된 타일 없어도 돼"

[해외 DS] 반세기 만에 찾은 ‘아인슈타인 타일’ ①, 아마추어 수학자의 놀라운 직관에서 이어집니다.

---

스미스는 처음부터 비주기적 모노타일을 찾으려는 구체적인 목표를 세우지는 않았지만, 이 문제의 역사와 중요성에 대해 잘 알고 있었다. 그는 타일 문제를 푸는 과정에서 비주기성의 징후를 항상 주시했었다.

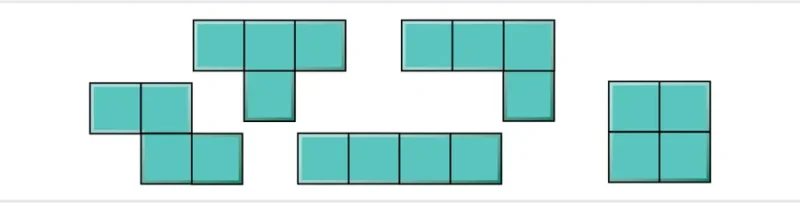
스미스와 카플란 교수는 모자의 행동을 이해하려고 노력하기 시작했다. 먼저 모자의 구성 요소를 살폈다. 이 모자는 폴리폼(polyform)이라고 불리는데, 어떤 단순한 단위 요소의 조합을 일컫는다. 예를 들어 ‘테트리스’ 게임의 모든 조각들은 네 개의 정사각형(단위 요소)을 다양하게 조합하여 만든 폴리폼들이다

모자 타일 속에 숨겨진 치환 규칙을 찾아서

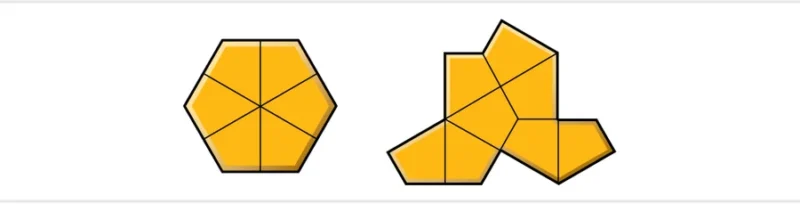
스미스의 모자는 8개의 연(kite)으로 만들어졌는데, 이 연은 펜로즈의 연과는 다르다. 스미스의 연은 정육각형을 6 등분 한 연으로 조합한 폴리폼이다.

스미스는 카플란 교수가 최근에 폴리오미노(정사각형을 붙여 만든 폴리폼), 폴리헥스(정육각형), 폴리아몬드(정삼각형)의 히쉬수를 계산하는 소프트웨어를 개발한 것을 알고 있었고, 이를 폴리카이트에 적용할 수 있는지 궁금해했다. 다행히도 카플란 교수는 워털루대학의 학부생인 아바 푼(Ava Pun)의 도움으로 연에 대한 기능을 추가한 적이 있었다.

카플란 교수의 소프트웨어는 막힘없이 큰 모자 클러스터를 쉽게 생성하여 모자가 평면을 타일링한다는 스미스의 믿음을 강화했다. 그뿐만 아니라 컴퓨터로 생성된 새로운 클러스터 이미지는 스미스의 직관을 개선할 수 있는 좋은 연구 자료가 되어 줬다. 그들은 디지털 일러스트레이션으로 직접 색칠하는 등 다양한 방법으로 모자를 그룹화하며 새로운 사실을 발견했다. 반사된 모자가 드문드문 배열되어 있고, 반사되지 않은 모자가 반사된 모자를 둘러싸는 반복 패턴이 튀어나온 것이다.

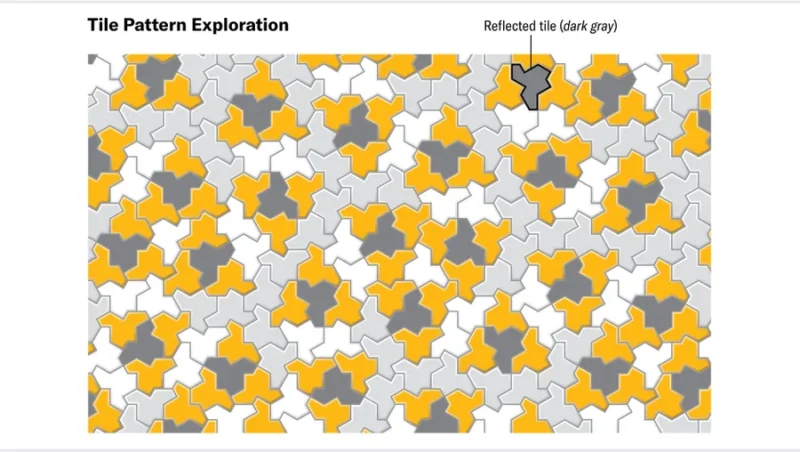
모자 타일의 이러한 패턴은 병진 단위를 형성하지 않으면서도 재귀적인 계층 구조를 가진 것처럼 보였다. 즉 반복되는 조합 패턴을 규정하고 해당 조합들을 재귀적으로 결합하면, 모양은 유지하면서 스케일은 무한대로 커질 수 있게 된다. 평면 타일링이 가능한 것이다. 결국 모자가 비주기적 타일일 수 있다는 것을 암시하는 최상의 시나리오였다. 한편 재귀적 계층 구조는 치환 규칙(substitution rules)이 적용된 시스템이다. 펜로즈의 타일 집합을 포함한 많은 비주기적 타일 집합에서 치환 시스템으로 평면을 타일링하는 것을 볼 수 있는데, 연과 다트로 구성된 펜로즈의 타일이 연과 다트의 조합 속에서 규모가 더 큰 연과 다트를 발견할 수 있는 시스템이다. 이런 식으로 모양이 변하지 않으면서 점점 더 큰 클러스터를 만들어가는 시퀀스를 발견하면 무한 평면을 채워 나갈 수 있다는 것을 증명할 수 있게 된다.

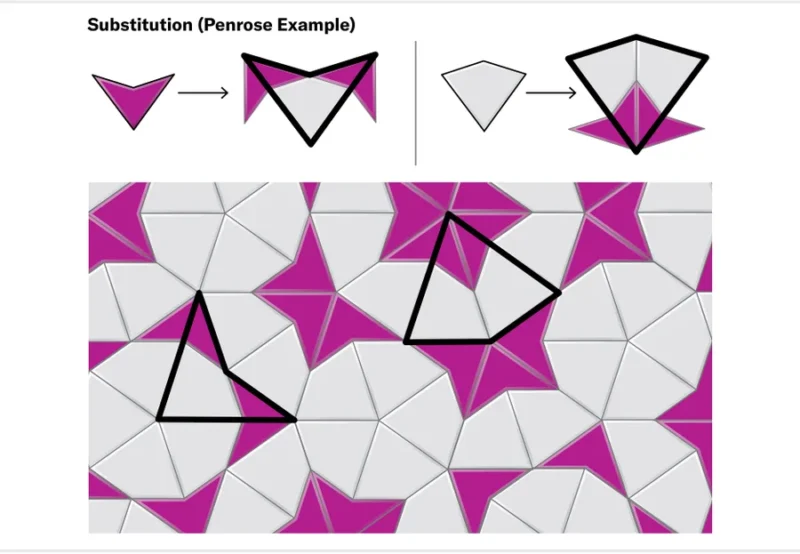
카플란 교수는 스미스의 이메일을 받고 약 2주가 흐른 시점에 모자 타일의 치환 규칙을 설명할 수 있을 ‘시드’ 구성을 발견했다. 비결은 반사된 모자는 반사되지 않은 모자와 다르게 행동할 수밖에 없기 때문에 단일 반사 모자로 직접 작업하는 것을 피하는 것이었다. 대신 반사된 모자를 세 개의 이웃 모자와 그룹화하여 분할할 수 없는 단위, 즉 자체적인 치환 규칙을 가진 타일 모양으로 취급할 수 있는 ‘메타타일’을 만들었다. 카플란 교수는 메타타일과 모자의 치환 규칙을 다듬어 4개의 메타타일(시드)로 구성된 치환 시스템을 정의했다.

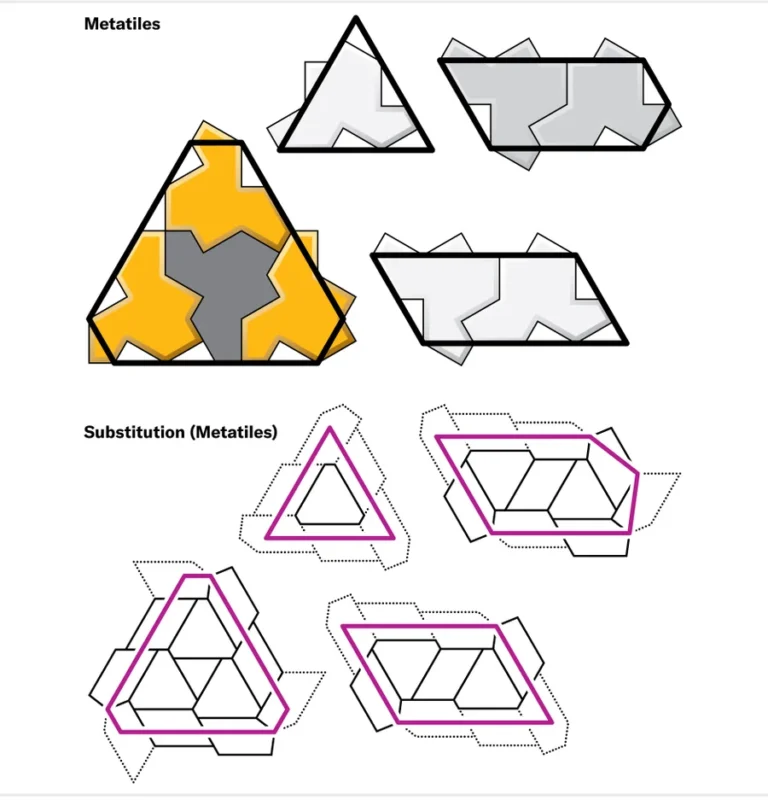
강한 비주기성을 증명하기 위해

스미스와 카플란 교수는 메타타일과 치환 규칙으로 모자가 모노타일이라는 것을 증명했다. 그리고 치환 규칙에 따라 생성된 타일링이 비주기적(nonperiodic)이라는 것도 쉽게 알 수 있었다. 하지만 강한 비주기성(aperiodic)은 담보할 수 없는 상황이었다. 강한 비주기성은 비주기적 타일이 임의로 큰 주기적 영역을 갖지 않아야 한다는 추가 속성이 있기 때문이다. 결국 모든 모자 타일링이 반드시 비주기적이라는 것을 증명하기 위해 2023년 1월 초 스미스와 카플란 교수는 타일링 이론에 관한 중요한 논문을 다수 발표한 수학자 굿맨-슈트라우스에게 연락을 취했다. 굿맨-슈트라우스는 수학 커뮤니케이터이자 타일링 체험 활동의 기획자로도 잘 알려져 있었고 그의 소개로 소프트웨어 개발자 조셉 사무엘 마이어스도 프로젝트에 합류했다.

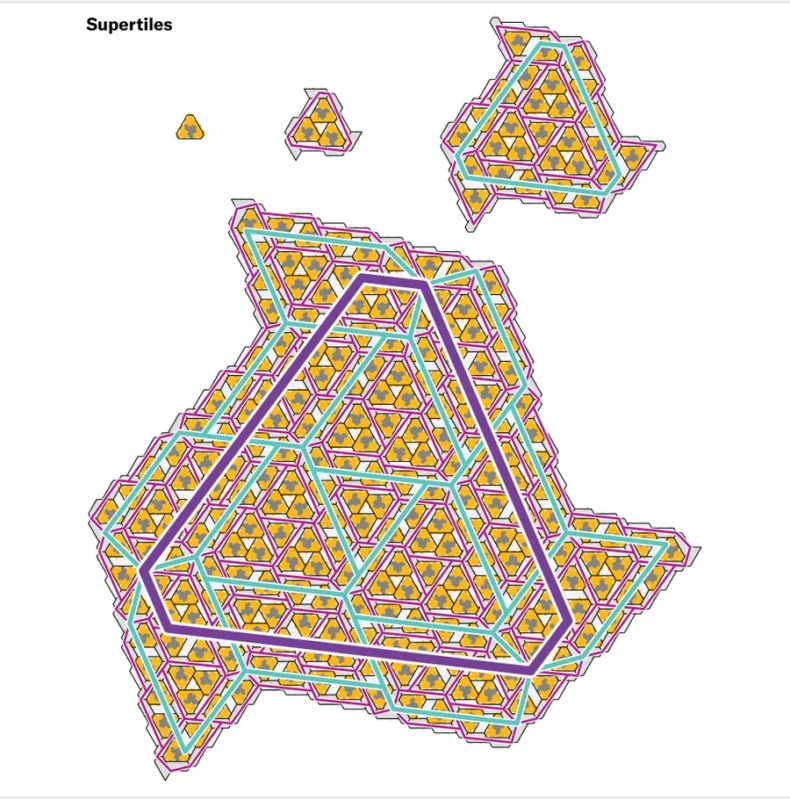
마이어스는 조합론으로 수학 박사 학위를 받은 후 학계를 떠났지만 타일링에 관한 관심은 계속 유지했다. 타일링에 대한 그의 이전 작업 덕분에 그는 불과 8일 만에 증명을 완료했다. 올해 1월 말에 이 모자가 세계 최초의 비주기적 모노타일임을 확인한 것이다. 그는 임의의 모자 타일이 메타타일로, 메타타일을 슈퍼타일로 그룹화하는 독특한 방법이 영원히 존재한다는 것을 증명하여 완전한 타일링으로 끝나는 치환의 무한 계층을 역설계해야 했다. 이를 위해 마이어스는 컴퓨터를 이용한 접근법을 개발했다. 모자 타일링에서 나타날 수 있는 188개의 작은 타일 클러스터를 생성하고, 각 클러스터를 고유한 방식으로 메타타일의 조각으로 나눌 수 있음을 보여줬다. 이는 어떤 모자 타일링도 메타타일로 분해할 수 있음을 의미한다. 마지막으로 그는 메타타일로 구성된 타일링에서 더 큰 메타타일처럼 동작하는 슈퍼타일로 클러스터를 확장할 수 있음을 보여줬다. 이 마지막 단계에서는 일종의 재귀가 시작되는데 슈퍼타일은 메타타일의 속성을 공유하기 때문에 동일한 그룹화 프로세스가 슈퍼타일에도 적용된다. 따라서 모자를 메타타일로 그룹화하고, 메타타일을 슈퍼타일로 그룹화하면 그 이후의 모든 계층은 수학적으로 일반화할 수 있다.

2022년 12월 스미스는 모자와 매우 유사한 특징을 가진 거북이라는 두 번째 비주기적 모노타일을 발견했다. 다른 사람들이 50년 동안 찾지 못하던 것을 스미스가 2주 만에 두 개의 모노타일을 발견하는 것이 가능한 일일까.

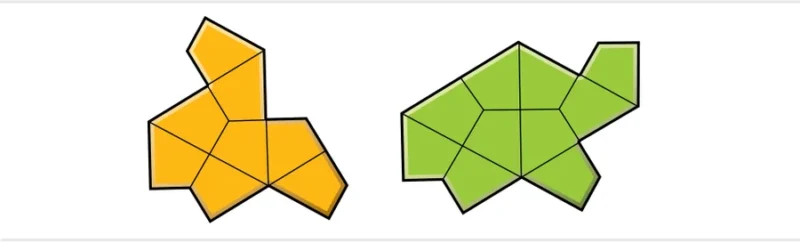
사실 모자와 거북이는 연속적인 다각형 계열의 두 도형이었으며, 모두 같은 방식으로 타일을 붙인 비주기적인 도형이다.

구체적으로 모자는 길이 1과 √3의 변으로 이뤄진 다각형이다. 사각형의 가로·세로 길이를 독립적으로 변경하여 여러 직사각형 계열의 도형을 생성할 수 있는 것처럼, 폴리카이트의 두 변(a와 b)을 Tile(a, b)라고 부르고 각각의 길이를 변경하면 새로운 다각형을 얻을 수 있다. 이 표기법을 사용하면 모자는 Tile(1,√3 )이 되고 거북이는 Tile(√3, 1)이 된다. 마이어스는 Tile(a, b) 형태의 거의 모든 도형이 동일한 타일을 가진 비주기적 모노타일임을 증명했다. 다만 세 가지 예외가 있었는데, Tile(0, 1)(‘갈매기’ 타일), Tile(1, 0)(‘혜성’ 타일), 그리고 정다각형 Tile(1,1)(별명은 얻지 못했다)이 바로 그것이다. 이 세 가지 도형은 각각 주기적 타일링과 비주기적 타일링을 모두 허용하는 보다 유연한 도형이기 때문에 비주기적 모노타일로 인정할 수 없었다.

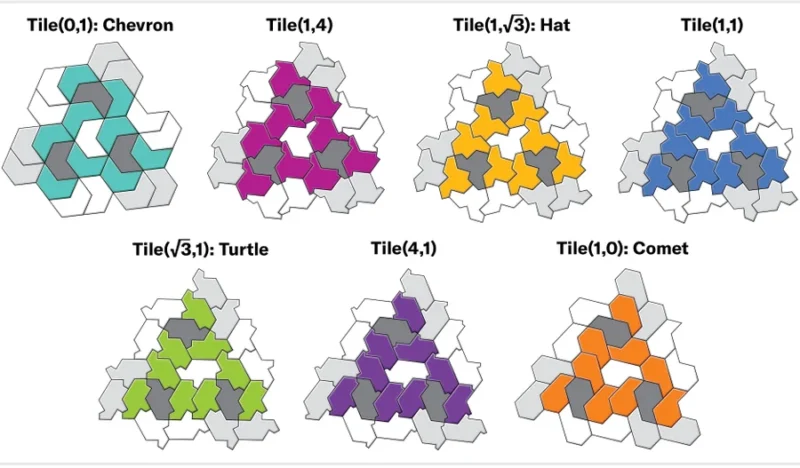
얼마 지나지 않아 마이어스는 모자와 거북이 사이의 연결 고리를 확장하여 Tile(a,b) 연속체를 기반으로 모자의 비주기성에 대한 새로운 증명을 개발했다. 그는 모순에 의한 증명 기법을 사용하여 모자의 주기적 타일링의 존재를 가정한 다음, 그러한 타일링의 존재로부터 처음 가정(모자의 주기적 타일링)이 불가능하다는 부조리를 도출해 냈다. 그는 먼저 주기적 모자 타일링의 가장자리를 늘이고 줄이면서 갈매기와 혜성에 의한 동등한 주기적 타일링을 얻을 수 있다는 것을 발견했다. 그러나 갈매기와 혜성은 모두 서로 다른 스케일의 정삼각형 타일링 위에 세워진 폴리아몬드(정삼각형의 결합)다. 마이어스는 조합론, 기하학, 그리고 약간의 정수론이 포함된 논증을 통해 갈매기와 혜성 타일링이 동일한 것으로 추정되는 주기적 모자 타일링에서 비롯됐기 때문에 단위 요소인 삼각형 타일링이 수학적으로 불가능한 배율을 통해 서로 연관되어야 한다는 것을 증명했다. 이것은 모자가 비주기적 모노타일이라는 것을 증명하는 새로운 방법이었다. 이는 모자의 비주기성에 관한 주장을 강화할 뿐만 아니라 이 분야에서 완전히 새로운 증명 방법을 제시하여 향후 다른 타일을 분석하는 데 유용할 수 있다는 점에서 시사하는 바가 크다.

유령 타일, 반사된 타일 없이 강한 비주기성 증명해

모자를 처음 공개했을 때 사람들은 다른 어떤 것보다도 반사 타일을 사용한다는 점을 가장 많이 지적했다. 스미스와 카플란 교수가 초기에 발견한 것처럼, 모자를 이용한 모든 타일링에는 반사된 모자가 드문드문 분포되어 있어야 한다. 모노타일의 정의는 반사 도형을 합법적인 움직임으로 허용해 왔었다. 그런데도 많은 사람들은 타일을 뒤집지 않는 ‘한 손’ 또는 ‘카이랄'(어떤 대상이 거울에 비춘 모양과 합동을 이루지 않을 때) 비주기적 타일링을 생성하는 도형이 존재할 수 있을까 궁금해했다.

다행히도 스미스는 놀라운 사실을 하나 더 알려줬다. 첫 번째 원고를 올린 지 일주일도 채 지나지 않아 그는 모자와 거북이를 포함하는 도형 연속체의 등변 Tile(1, 1)에 대해 이메일을 보내기 시작했다. 메일을 받은 세 명 모두 해당 다각형은 비주기적 타일이 아니라 무반사 타일과 반사 타일이 섞인 주기적 타일이라는 것을 알고 있었다. 하지만 스미스는 의도적으로 한 손으로만 뒤집는 타일로 반사를 제한하면 흥미로운 타일 군집이 만들어지는 것을 관찰했다.

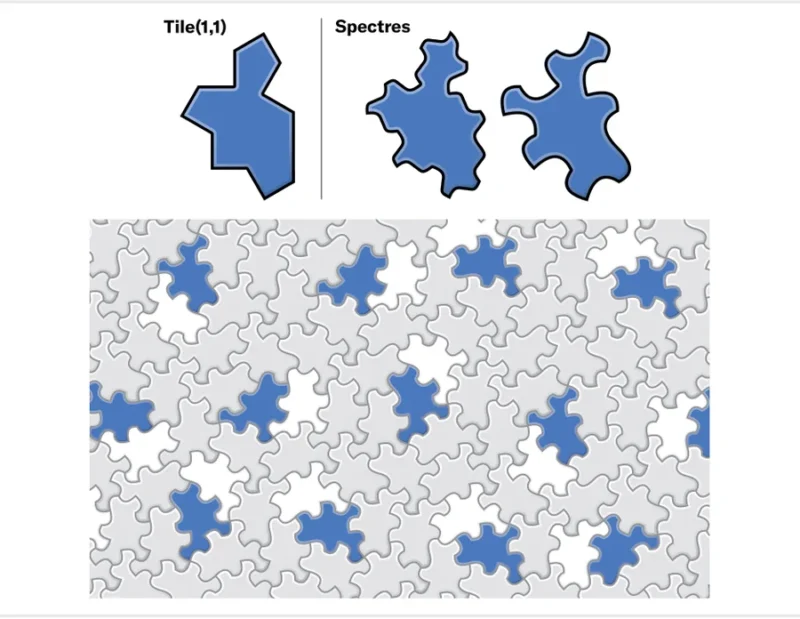
네 사람은 즉시 연구를 시작했다. 그들은 Tile(1,1)의 반사되지 않은 복사본의 메타타일을 계산하고, 타일을 반복되는 클러스터로 그룹화하는 방법을 발견한 다음, 동일한 성질을 갖는 슈퍼타일을 생성하는 치환 시스템을 정리했다. 그 결과 그들은 다시 한번 비주기적 타일링을 강제하는 고유한 무한 치환 계층의 존재를 반사되지 않은(한 손) 타일에서도 발견했다. 마지막으로 Tile(1,1)의 가장자리를 임의의 곡선으로 대체하여 기존 타일과 그 반사 타일이 공존할 수 없도록 설정했다. 이를 유령(spectres) 타일이라고 부르고, 모든 임의의 유령 타일은 카이랄 비주기적 모노타일임을 밝혔다.

카플란 교수는 “항상 아인슈타인 문제에 매료됐지만 직접 연구한 적은 없었고, 2022년 11월에 해답을 받은 후에야 시작했습니다. 모자는 스미스의 손에서 어느 정도 구체화됐고, 운이 좋게도 그가 연락을 줬습니다. 몇 달 후 우리는 어렵지 않게 완전한 증거를 만들 수 있었는데, 네 명 모두 수십 년 동안 아인슈타인 문제와 관련된 질문에 대해 고민해 온 노력의 보상 같습니다”라고 소감을 밝혔다.

---

Smith hadn’t specifically set out to find an aperiodic monotile, but he was aware of the history and significance of the problem. He was always on the lookout for signs of aperiodicity in his explorations. It was Smith who first dared to suggest, in an e-mail on November 24, 2022, that the hat might be an einstein, modestly adding, “Now wouldn’t that be a thing?”

Smith and I began trying to understand the hat’s behavior. The hat is what’s known as a polyform: a shape made up of copies of some simple unit element. For example, the pieces in the video game Tetris represent all the ways to stick four squares together.

The hat is made from eight kites. These kites aren’t the same as Penrose’s; Smith made them by slicing a regular hexagon into six equal pieces with lines connecting the midpoints of opposite edges.

He knew that I had recently written software to compute Heesch numbers of polyominoes (glued-together squares), polyhexes (regular hexagons) and polyiamonds (equilateral triangles), and he wondered whether it could be adapted to polykites. Fortunately, I had added support for kites the year before with the help of Ava Pun, an undergraduate at the University of Waterloo.

My software easily generated large clusters of hats without getting stuck, reinforcing our belief that the hat tiled the plane. Better yet, these new computer-generated clusters became raw data that Smith and I could study to refine our intuition. We began grouping hats in different ways, usually coloring them by hand in digital illustrations, to search for order. Recurring patterns leaped out immediately, organized around a sparse arrangement of reflected hats embedded in a larger field of unreflected hats (something Smith had also observed in his paper experiments).

Yet these patterns never formed a translational unit. Moreover, the tiles seemed to build up into families of related “motifs” at multiple scales. This kind of recurring hierarchy hinted at a best-case scenario for eventually proving the hat was aperiodic: we could hope to find a system of so-called substitution rules. In a substitution system, every tile shape in a set is equipped with a rule that can be applied to replace it by a collection of smaller copies of the tiles. Armed with a suitable substitution system for hats, we might be able to start with a “seed” configuration of tiles and apply the rules iteratively, zooming in as we go to preserve scale. In this way, we would define a sequence of ever-larger clusters of hats, which would eventually fill the entire plane. Many aperiodic tile sets, including Penrose’s, can be shown to tile the plane with substitution systems like these.

On my 50th birthday, about two weeks after I first saw the hat, I found a preliminary set of substitution rules. The trick was to avoid working directly with “naked,” or single, reflected hats, which necessarily behaved differently than their unreflected counterparts. Instead I grouped each reflected hat with three of its neighbors to form an indivisible unit, a new “metatile” that could be treated as a full-fledged tile shape with a substitution rule of its own. I refined the metatiles and their rules through the rest of 2022, arriving at a system of four metatiles, each one a kind of schematic representation of a small cluster of hats.

By the start of 2023 Smith and I had half of a proof of aperiodicity, and arguably it was the easy half. Our metatiles and substitution rules guaranteed that the hat was a monotile: it tiled the infinite plane rather than petering out with an unexpectedly large, but finite, Heesch number. And it was easy to see that the tilings generated by the rules were nonperiodic. But remember that nonperiodicity is a far cry from aperiodicity. Perhaps our rules were just an overly complicated way to construct hat tilings, and periodic tilings existed, too. To complete the proof, we had to show that every tiling by hats was necessarily nonperiodic. I had some inkling of how that step might play out, but I felt as I imagine Smith had the previous November: close to the limits of my mathematical expertise. It was time to call in reinforcements.

Early in January 2023 Smith and I reached out to Goodman-Strauss, a mathematician who has published many important articles about tiling theory. I consider him a go-to authority on contemporary research. He is also known as a mathematics communicator and an organizer of hands-on activities, and at the time he was transitioning into a new role as an outreach mathematician at the National Museum of Mathematics in New York City. In other words, he was already swamped. But he provided valuable input and insisted that we also contact Myers immediately. Myers left academia after receiving a Ph.D. in the mathematical field of combinatorics, but he remained interested in tilings. In particular, he maintained a long-term project to catalog the tiling properties of polyforms. I had run some supporting computations for him back in 2006, and I was using his software as part of my own research on Heesch numbers.

I hadn’t worked that closely with Myers before, so I was unprepared for his combination of mental horsepower, coding skill and knowledge of the field. His previous work on tilings had left him perfectly prepared for this moment. A mere eight days after being introduced to our work in progress, Myers completed the proof, confirming in late January that the hat was the world’s first aperiodic monotile.

Before Myers came onboard, we already had our substitution rules and could generate tilings; his mission was to prove that all tilings by the hat had to be nonperiodic. In the aperiodicity playbook, the standard move at this point is to show that any tiling bears the imprint of the substitution rules. In other words, he needed to prove that for any arbitrary hat tiling, there is a unique way to group tiles into metatiles, metatiles into supertiles, and so on forever, reverse-engineering an infinite tower of substitutions that ends with the full, infinite tiling. A preexisting mathematical argument then would allow us to conclude that the tiling must be nonperiodic. The challenge of this strategy is to locate this tower atop an arbitrary hat tiling whose construction was not constrained at the outset to obey our rules.

Myers developed a computer-assisted approach to solving this problem. We generated an exhaustive list of 188 small clusters of tiles that could appear in hat tilings. These clusters represented every legal arrangement around a single hat so that each tile in any conceivable tiling must lie at the center of one such cluster. Myers then showed that each of these clusters could be divided up in a unique way into fragments of the metatiles, implying that the hats in any tiling could be grouped to yield a tiling by metatiles. Finally, he demonstrated that in a tiling made of metatiles, it was always possible to group metatiles into larger clusters called supertiles, which behave exactly like larger metatiles. This last step launches a kind of recursion: because the supertiles behave just like metatiles, the same grouping process applies to them as well. Once we group hats into metatiles and metatiles into supertiles, all subsequent levels of the hierarchy lock into place with a single mathematical flourish.

We had our prize, and in early February 2023 we began writing a manuscript to share the hat with the world. That might have been the end to an already magical story were it not for Smith’s capacity for mathematical discovery. Way back in December 2022 he had shocked me by e-mailing me a second shape, a polykite we call the turtle, which behaved a lot like the hat. The turtle, too, radiated an uncanny aura of aperiodicity. Was it possible that Smith had discovered two revolutionary shapes in two weeks after others had looked in vain for 50 years? I begged for patience; my head was already full of hats, so to speak.

But after resolving the status of the hat, Myers began contemplating the neglected turtle. A week or two later he stunned the three of us with the observation that the turtle was necessarily also aperiodic because it was really just a hat in disguise. In fact, the hat and the turtle were two shapes in a continuous family of polygons, all of which were aperiodic and tiled in the same way.

The hat can be regarded as a polygon with edges of length 1 and √3 (where two consecutive edges of length 1 form one longer edge). Just as one can construct a family of rectangles by varying the lengths of its horizontal and vertical edges independently, we can choose any two numbers a and b to replace the hat’s edge lengths and obtain a new polygon that we will call Tile(a,b). Using this notation, the hat is Tile(1, √3), and the turtle is Tile(√3, 1). Myers showed that nearly all shapes of the form Tile(a,b) are aperiodic monotiles with the same tilings. There were just three exceptions: Tile(0,1) (the “chevron”), Tile(1,0) (the “comet”) and the equilateral polygon Tile(1,1) (which never acquired a catchy nickname). Each of these three shapes is more flexible, admitting both periodic and nonperiodic tilings.

Soon after, Myers doubled down on the link he had forged between the hat and the turtle, developing a remarkable second proof of the hat’s aperiodicity based on the Tile(a,b) continuum. He relied on the classic technique of proof by contradiction: he posited the existence of a periodic tiling of hats, and then, from the existence of such a tiling, he derived an absurdity that showed the initial supposition (the periodic hat tiling) was impossible. Specifically, he found that one could stretch and squeeze edges in a periodic hat tiling to obtain equivalent, periodic tilings by chevrons and comets. But chevrons and comets are both polyiamonds (unions of equilateral triangles) built on top of regular triangular tilings at different scales. In an argument that involves combinatorics, geometry and a dash of number theory, Myers proved that because the chevron and comet tilings originated from the same supposedly periodic hat tiling, their underlying triangle tilings would have to be related to each other through a mathematically impossible scaling factor. This was a second way to prove that the hat is an aperiodic monotile. It’s exciting not just because it bolsters the claim of the hat’s aperiodicity but also because it represents a whole new method of proof in this field, which could be useful in analyzing other tiles in the future.

We put our manuscript online in March 2023 and received an enthusiastic, overwhelming response from mathematicians and tiling hobbyists. The hat became an immediate source of inspiration for artists, designers and puzzle creators (you can now buy hat tiling sets on Etsy, for instance). It’s important to remember that the work has not yet emerged from the crucible of peer review, although it has withstood a great deal of scrutiny from experts with barely a scratch.

When we first revealed the hat, people objected to one aspect of our work more frequently than any other: the use of reflected tiles. Every tiling by hats must include a sparse distribution of reflected hats, as Smith and I discovered early on. Mathematically, this objection does not derail our result: the accepted definition of a monotile has always allowed reflections as legal moves in tilings. Still, many wondered, could there be a shape out there that yields a “one-handed,” or “chiral,” aperiodic tiling in which no tiles are flipped over? Our manuscript offered no insight into this problem, and we were as prepared as everyone else to settle in for the long wait until its resolution.

Happily, Smith had one more astounding surprise for us. Less than a week after our first manuscript went live, he began e-mailing the rest of us about Tile(1,1), the equilateral member of the continuum of shapes that included the hat and the turtle. We knew that this polygon was not aperiodic: it admitted periodic tilings that mixed unreflected and reflected tiles. But Smith observed that if he deliberately restricted himself to tiles of a single-handedness (no flipping allowed), he produced intriguing clusters of tiles.

The four of us immediately dove into a new collaboration. We computed large patches of unreflected copies of Tile(1,1) and studied them for patterns. We discovered a way to group tiles into recurring clusters and then determined substitution rules for those clusters that yielded superclusters with identical behavior. Once again, this recursive grouping guaranteed the existence of a unique infinite hierarchy of substitutions that forced all unreflected (single-handed) tilings to be nonperiodic. The final trick was simply to replace the edges of Tile(1,1) with arbitrary curves, which guaranteed that tiles and their reflections couldn’t coexist in a tiling. The result was a family of shapes that we called spectres, all of which turned out to be chiral aperiodic monotiles.

There is a romance to stories of mathematicians working for years on intractable problems, sometimes in secret, and finally emerging into the light with a new result. That is not our story. Although I was always fascinated by the einstein problem, I never worked on it directly—I started only when I was handed the answer in November 2022. The hat more or less materialized in Smith’s hands, and I was lucky that he chose to contact me. A few months later we had a complete proof, created through a process that was, as far as I can tell, painless for all four of us. Perhaps our pace reflects the fact that there is a clear procedure to follow in generating a proof of aperiodicity if you have the right shape to begin with. Our sense of ease was also surely a result of the decades we had each spent pondering the einstein problem and related questions. That experience left us well positioned to recognize the hat as a possible solution and to know what to do with it.

There is no shortage of unsolved problems in tiling theory, a branch of mathematics with a low barrier to entry and lots of visual appeal. Smith joins a pantheon of enthusiastic amateurs who have made important contributions to the field, often after reading about open problems in this magazine. He is in the company of Robert Ammann, who independently discovered many of the same results as Penrose and contributed other important ideas to tiling theory; Marjorie Rice, who discovered new classes of pentagonal monotiles; and Joan Taylor, who originated the Socolar-Taylor tile. I should also include the artist M. C. Escher, who invented the math he needed to draw his tessellations, even if he would not have thought of it as math at all.

As the impact of our aperiodic monotiles ripples outward, I’m sure it will stimulate new scholarly research. But I hope we also entice others who might have seen mathematics as forbidding but now recognize an opportunity to play.