[해외 DS] 마이크로소프트 수학 전용 SLM ‘오르카-매쓰’ 발표, LLM과 기존 모델 모두 능가
오르카-매쓰는 미스트랄 7B 모델 기반으로 만들어졌으며, GSM8K 벤치마크에서 LLM과 기존 수학 전용 모델을 모두 능가해 주요 성공 요인은 고품질 합성 데이터, 반복 학습, SFT-KTO-KTO 시퀀스를 활용한 교사의 피드백 품질 향상에 있어 마이크로소프트는 20만 단어의 AI 생성 합성 수학 문제 세트를 허깅페이스에 공개

마이크로소프트 리서치(이하 MS)에서 수학 전문 언어 모델 ‘오르카-매쓰'(Orca-Math, 이하 오르카)를 발표했다. 오르카는 소형언어모델(SLM)로 수학 문제 해결에 있어 제미나이 프로(Gemini Pro) 및 GPT-3.5와 같은 대형언모델(LLM)보다 뛰어난 성능을 기록하여 특정 도메인에 특화된 SLM의 잠재력을 뽐냈다.
수학 문제 해결 능력에서 LLM과 기존 수학 전용 모델을 모두 능가
‘미스트랄 7B'(Mistral 7B) 모델을 기반으로 만들어진 오르카는 GSM8K pass@1에서 86.81%라는 놀라운 성과를 거두며 메타, 구글, 오픈AI의 모델 성능을 추월했다. GSM8K는 인간 작성자가 만든 8.5만 개의 초등학교 수준의 수학 문제로 구성된 고품질 데이터 세트다. 주로 기본 산술 연산(+ – ×÷)을 사용하여 일련의 계산을 수행해 최종 답에 도달하는 방식으로 푸는 문제다. 영리한 중학생이라면 모든 문제를 풀 수 있어야 하는 수준이다.
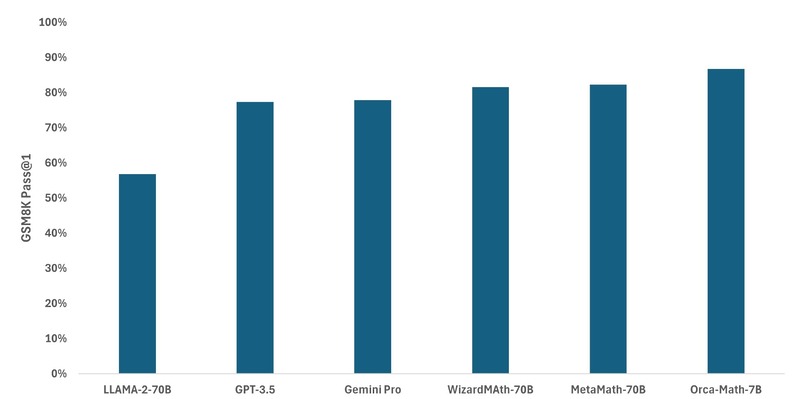
오르카는 LLM보다 높은 성능을 보였을 뿐만 아니라, MetaMath-70B 및 WizardMa8th-70B와 같은 다른 수학 전용 모델과의 경쟁에서도 우위를 지켰다. 또한 AddSub, MultiArith, SinglEq와 같은 다른 수학 데이터 세트에서도 강력한 성능을 보여줬다. 수학 문제를 푸는 것이 SLM에게 오랫동안 복잡한 작업으로 인식되어 왔던 걸 미루어 보면 괄목할 만한 성과라는 평이 납득이 가는 이유다.
더 작은 모델로 더 높은 수준의 성능을 달성하기 위해 연구자들은 종종 SLM을 훈련시켜 코드를 생성하거나 계산기를 사용하여 계산 오류를 방지한다. 아울러 모델을 최대 100회까지 호출하여 각 호출마다 문제 해결을 다시 시도하는 앙상블이라는 기법을 사용하는데, 앙상블을 사용하면 정확도가 크게 향상되지만, 모델을 여러 번 호출하기 때문에 컴퓨팅 비용이 크게 증가하는 문제점이 있다. 오르카 연구진에 따르면 이번 연구는 수학 문제 해결에 특화된 SLM이 외부 도구, 검증자 또는 앙상블을 사용하지 않고도 얼마나 더 높은 수준의 능력을 발휘할 수 있는지 탐구하는 것을 목표했다고 한다.
고품질 합성 데이터와 반복 학습
먼저 MS 연구진은 오르카의 성공 요인을 고품질의 합성 데이터로 꼽았다. 시드 문제를 기반으로 다양한 수와 속성을 가진 문제를 생성하면 작은 모델을 위한 학습 데이터를 생성할 수 있다. 연구진은 자동 생성 기능을 사용하여 새로운 문제와 솔루션을 생성하는 다중 에이전트로 풀이법을 더 많이 만들 수 있었을 뿐만 아니라 문제의 다양성과 난이도도 높일 수 있었다. 구체적으로는 제안자(suggester)와 편집자(editor) 에이전트를 사용했는데, 제안자는 문제를 검토하고 복잡도를 높이기 위한 방법을 제안하고, 편집자는 원래의 문제와 제안자의 추천을 참고해 더 어려운 문제를 생성하는 방식이다. 이러한 과정은 여러 라운드에 걸쳐 진행될 수 있으며 각 라운드마다 문제의 난이도가 높아진다. 마지막으로 제삼의 에이전트는 문제가 해결 가능한지 확인하고 해결책을 만든다.
학습 데이터의 구조에 맞게 학습 과정도 마찬가지로 교사(LLM)와 학생(SLM) 간의 반복학습이 이루어진다. 마치 실제 학생이 교사로부터 수학 문제 풀이법을 배우듯이 학생 모델은 먼저 교사 모델의 시범을 통해 풀이법을 배운다. 그런 다음 학생 모델은 스스로 문제 해결을 연습하고 교사 모델은 그에 맞는 피드백을 제공하며, 여기엔 동일한 문제에 대한 좋은 해결책과 나쁜 해결책을 모두 보여주는 선호도 데이터가 포함된다. 피드백을 받은 학생 모델은 해당 내용을 참고해 더 좋은 풀이법을 만들어내고 이러한 프로세스는 반복적으로 진행된다. 물론 여러 번 시도한 후에도 학생 모델이 문제를 올바르게 해결할 수 없는 경우, 교사가 제공한 솔루션을 사용하도록 설정됐다.
교사의 피드백 품질이 핵심, ‘SFT-KTO-KTO’
결국 교사의 피드백이 학생의 능률을 좌우한다. 하지만 인간을 통해 “입력 X에 대해 출력 A가 B보다 낫다”라는 피드백을 만드는 비용이 만만치 않다. 게다가 인간의 판단이 주관적이기 때문에 결과가 상충될 수 있어 우리가 익히 알고 있는 LLM의 편향·환각·유용성 및 해석 가능성 부족 등의 증상이 나타난다. 따라서 MS 연구팀은 기존의 감독 하의 미세조정(Supervised Fine-Tuning, 이하 SFT)과 더불어 성능 저하 없이 쉽고 저렴하게 LLM을 정렬할 수 있는 카네만-트베르스키 최적화(Kahneman-Tversky Optimization, 이하 KTO)라는 방법을 차용했다.
KTO는 작년 말 스타트업 컨텍스츄얼 AI(Contextual AI)가 개발하여 오픈소스로 공개한 얼라인먼트 기법으로, 인간의 의사결정에 대한 경제학자 카네만과 트베르스키의 연구를 통해 “입력 X에 대해 출력 Y가 바람직한지 바람직하지 않은지”만 물어본다. 이러한 종류의 피드백은 적용 범위가 넓은 장점이 있다. 예로 들어 모든 회사에는 바람직한(예: 판매가 이루어짐) 또는 바람직하지 않은(예: 판매가 이루어지지 않음) 것으로 표시할 수 있는 고객 상호 작용 데이터가 있다. 이번 연구의 리더이자 MS의 선임 연구원인 아린담 미트라(Arindam Mitra)에 따르면 SFT로 시작하여 두 차례의 KTO로 이어지는 ‘SFT-KTO-KTO’ 시퀀스가 연속적인 SFT 시퀀스보다 더 효과적이었으며 DPO(Direct Preference Optimization는 수학적으로 RLHF와 동등하면서도 훨씬 간단하여 오픈소스에서도 얼라인먼트가 용이한 강화학습 기법)도 뛰어넘는 것으로 입증됐다.
한편 MS의 오르카 연구팀은 상업적 용도로도 “누구나 탐색, 구축 및 혁신”할 수 있도록 허용하는 MIT 라이선스에 따라 20만 단어로 구성된 AI 생성 합성 수학 문제 세트를 허깅페이스(Hugging Face)에 게시했다. 따라서 스타트업과 기업에서 이를 활용할 수 있게 됐다. 특히 LLM의 개발·유지 비용을 감당하기 어려운 기업이 대다수인 만큼 적용 대상이 넓을 것으로 예상된다.