[해외 DS] ‘가공할 헛소리’를 증명한 끈 이론 ①, 수학자의 뇌리에 박힌 숫자 ‘196,884’
존 맥케이, 기하학 및 정수론과 관련된 숫자 '196,884' 발견 존 톰슨, 맥케이의 주장에 힘을 실어줄 두 번째 숫자 찾아 두 분야의 연관성을 추측한 '가공할 헛소리'라는 제목의 논문 발표
[해외DS]는 해외 유수의 데이터 사이언스 전문지들에서 전하는 업계 전문가들의 의견을 담았습니다. 저희 데이터 사이언스 경영 연구소 (GIAI R&D Korea)에서 콘텐츠 제휴가 진행 중입니다.

오랫동안 사람들은 고(故) 존 맥케이(John Mackay)가 수비학에 매료되거나 바더-마인호프 현상을 경험하고 있다고 추측했다. 사람들의 오해를 불러일으킬 정도로 그가 집착했던 숫자는 196,884였다.
눈앞에 아른거리는 숫자 ‘196,884’
맥케이는 1978년 자신의 전공이 아닌 수학 분야의 논문을 살펴보던 중 우연히 이 숫자를 발견했다. 그는 기하학을 전공하고 있었고 도형의 대칭을 연구하고 있었다. 소수와 같은 정수의 성질을 다루는 정수론의 결과를 살펴보던 중, 그의 눈에 196,884라는 값으로 시작하는 일련의 숫자가 들어왔다.
맥케이는 이 숫자가 낯익었다. 그는 이전에 ‘괴물'(Monster)이라고 알려진 수학적 구조(당시에는 가설에 불과했다)를 연구한 적이 있었는데, 이 기묘한 대수 구조는 196,883개 차원(숫자 196,884보다 하나 적은 차원)에 존재하는 기하학적 물체의 대칭성을 설명하기 위한 것이었다. 1차원의 점은 모든 대칭을 충족하기 때문에 그는 괴물의 대칭성이 적용된다고 믿었던 처음 두 차원을 더해서 196,883 + 1 = 196,884를 다시 만났다.
전문가들은 맥케이의 발견에 관심을 기울이지 않았다. 괴물과 같은 구조는 수많은 숫자를 포함하고 있으며, 마찬가지로 수 이론의 결과도 많은 숫자를 포함했다. 그중 몇 개는 우연에 의해 서로 같을 수 있다며 대수롭지 않게 넘겼던 것이다.
하지만 맥케이는 기하학과 정수론이 극도로 다른 두 수학 분야지만 서로 긴밀한 연관성이 있다는 느낌을 떨쳐버릴 수 없었다. 심지어 그는 컨퍼런스에서 “196,883 + 1 = 196,884″라는 문구가 적힌 티셔츠를 입기도 했다.
한 수학자의 광기일까 아니면 천재적인 발상일까?
얼마 후 존 톰슨(John Thompson)은 맥케이의 의구심에 결국 뭔가가 있을지도 모른다는 것을 깨달았다. 그는 괴물의 대칭을 따르는 한 물체의 다음 차원과 수 이론에 등장하는 그 신비한 수열의 다음 항을 연결하는 데 성공했다. 그 차원은 21,296,876인데, 값은 다르지만 이전과 같이 모든 괴물의 차원을 더하면(1 + 196,883 + 21,296,876) 결과는 21,493,760이 된다.
맥케이가 봤던 그 수열의 두 번째 항이 바로 21,493,760으로 톰슨의 결과와 일치했다. 전혀 관련이 없어 보이는 두 수학 영역 사이에 실제로 연결 고리가 있을 수 있다는 생각이 들기 시작한 것이다. 수학 커뮤니티도 호기심을 갖기 시작했다. 상상할 수 없이 큰 물체(괴물)의 대칭을 설명하는, 아직 완전히 구성되지도 않은 이 기묘한 구조가 수 이론과 도대체 무슨 관련이 있을까?
1979년에 이르러 다른 수와 차원도 이 예상치 못한 패턴을 따르는 것 같다는 증거가 쌓여갔다. 수학자 존 콘웨이(John Conway)와 사이먼 노턴(Simon Norton)은 마침내 기하학과 수론 사이의 연관성에 대한 추측을 담은 ‘가공할 헛소리'(Monstrous Moonshine)이라는 제목의 논문을 발표했다. 독일 본에 있는 막스 플랑크 수학연구소의 수 이론가인 돈 자기에(Don Zagier)는 2015년 퀀타 매거진과의 인터뷰에서 “너무 억지스러워 보였기 때문에 가공할 헛소리라고 불렀다”고 언급했다.
그리고 실제로 이 추측을 증명할 수 있는 희망은 거의 없었다. 서로 멀리 떨어져 있는 두 수학 영역이 서로 연결되어 있다는 증거가 없다는 사실 외에도 괴물이 실제로 존재한다는 사실조차 완전히 밝혀지지 않았기 때문이다.
달빛 속의 괴물
괴물은 물체의 대칭적 성질을 다루는 기하학의 한 분야인 군론의 이론적 예측이다. 1970년대에 수학자들은 일종의 주기율표를 만들기 시작했는데, 유한 대칭의 ‘원자’를 찾고자 했다. 원자들을 찾으면 그 조합으로 모든 유한한 그룹을 나타낼 수 있었기 때문이다. 수십 년간의 연구 끝에 기하학자들은 마침내 목표에 도달한 것처럼 보였다. 화학 원소와 달리 ‘유한 단순 그룹’은 무한히 많지만 거의 모두 18개의 범주로 나눌 수 있으며 주기율표를 연상시키는 배열로 표현됐다. 또한 전문가들은 이 18개 범주에 맞지 않는 26개의 산재군을 발견했다.
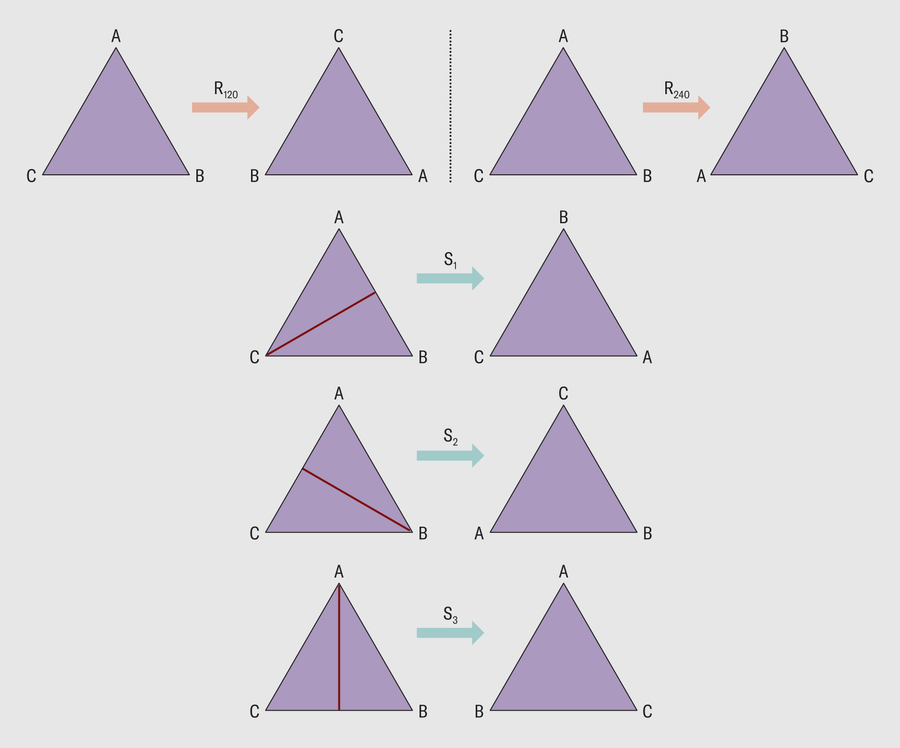
이 중 첫 번째 산재군이 1973년 수학자 베른트 피셔(Bernd Fischer)와 로버트 그리스(Robert Griess)가 예측한 ‘괴물‘이었다. 괴물이라는 이름은 해당 그룹의 엄청난 크기에서 유래했는데, 이 그룹에는 8×1053개 이상의 대칭이 포함돼 있다. 비교를 위해 20면체 ‘D20’ 주사위(an icosahedron)를 예로 들면, D20의 대칭 그룹은 60개의 대칭을 포함하는데, 이는 D20의 방향을 바꾸지 않고도 60가지 변형(회전 또는 반사)을 수행할 수 있다는 것을 의미한다.
그 거대함 때문에 괴물군은 수학자들에게 큰 난제를 안겨주었다. “당시에는 더 작은 그룹이라도 컴퓨터로 구축해야 했기 때문에 대부분의 사람들은 이 괴물을 만드는 것이 절망적이라고 생각했다”고 이 분야에 큰 공헌을 한 수학자 리처드 보처즈(Richard Borcherds)는 Monstrous Moonshine에 대한 설명이 담긴 유튜브 동영상에서 이렇게 말했다. 하지만 1980년 그리스는 컴퓨터의 도움 없이도 괴물을 만들어 그 존재를 증명했다.
[해외 DS] ‘가공할 헛소리’를 증명한 끈 이론 ②, 복잡하지만 아름다운 수학과 물리의 대칭성으로 이어집니다.
영어 원문 기사는 사이언티픽 아메리칸에 게재되었습니다.