[해외 DS] 암호화된 ‘비밀 공유’, 정보를 안전하게 보호하는 방법
샤미르의 비밀 공유, 다수의 참여자가 협력해야만 암호를 풀 수 있었 다항식의 성질을 활용해 참여자의 숫자에 상관없이 일반화가 가능해 만에 하나의 가능성을 배제하기 위해 숫자 범위를 유한체로 전환
[해외DS]는 해외 유수의 데이터 사이언스 전문지들에서 전하는 업계 전문가들의 의견을 담았습니다. 저희 데이터 사이언스 경영 연구소 (GIAI R&D Korea)에서 영어 원문 공개 조건으로 콘텐츠 제휴가 진행 중입니다.

러시아 속담인 ‘신뢰하되 검증하라’는 냉전 시대 미국 대통령인 로널드 레이건이 핵 군축을 언급할 때 자주 사용한 말이다. 이는 미국이 소련을 신뢰할 수 있지만, 소련이 미국을 배신하지 않을지 확인해야 한다는 의미를 내포하고 있다. 이 속담은 오늘날 국가 안보 및 보안 분야에서 자주 활용되며, 수학자 아디 샤미르(Adi Shamir)는 자신의 이름을 딴 ‘샤미르의 비밀 공유(Shamir’s Secret Sharing, 이하 SSS)’ 알고리즘을 개발할 때 이러한 속담의 의미를 한 번쯤 생각해 봤을 것이다.
샤미르의 보안 메커니즘을 이해하기 위해서는 다음과 같은 상황을 이해하는 것이 도움이 된다. 한 노파가 비밀번호 자물쇠로 잠긴 금고의 내용물을 다섯 아들에게 물려주고 싶지만, 모든 아들을 신뢰하지 않는 상황을 가정해 보자. 이 노파는 한 명의 아들에게만 비밀번호를 알려주면 그 아들이 유산을 훔쳐 달아날까 걱정이다. 그래서 그녀는 5명의 아들이 협력하여 금고를 열 수 있도록 각 아들에게 단서를 주려고 한다. 예를 들어, 5자리 비밀번호가 있어야 하는 잠금장치라면 각 아들에게 숫자 한자리씩 주어 함께 열 수 있도록 설계할 수 있다. 그러나 세 아들이 팀을 이루면 나머지 두 형제를 우회할 가능성이 있으며, 세 아들은 전체 코드의 숫자가 두 개만 부족하므로 유산을 얻기 위해 가능한 숫자 조합을 빠르게 시도할 수 있다는 문제점이 있다.
노파는 5명이 모두 협력하지 않으면 사용할 수 없는 암호 설계 방법을 모색했다. 5명의 아들 중 2, 3, 4명이 함께해도 그 결과는 쓸모없는 정보여야만 한다. 이런 제약 사항은 작업을 더욱 복잡하게 만들었지만, 1979년 샤미르는 이러한 어려움에도 굴하지 않았다. 그는 2년 전(1977년), 로널드 라이베스트(Ron Rivest)와 레너드 애들먼(Leonard Adleman)과 함께 ‘RSA 알고리즘’이라고 불리는 암호 알고리즘을 개발했다. 이 알고리즘은 처음으로 널리 채택된 비대칭 암호화 알고리즘이었고, 오늘날에도 여전히 사용되고 있다. SSS 알고리즘으로 또 한 번 혁신적인 방법을 창조함으로써 보안 분야에서 중요한 발전을 이뤘다.
샤미르의 비밀 공유, 좌표평면 위에서 이뤄지는 간단한 일반화
SSS를 이해하기 위해서는 구체적인 수치 예시를 살펴보는 것이 도움이 된다. 노파의 비밀 코드가 43953이고, 편의상 그녀에게 아들이 두 명만 있었다고 가정해 보자. (아들이 다섯 명인 경우는 아래에서 설명한다). 만약 노파가 한 아들에게 “439”를, 다른 아들에게 “953”을 맡겼다고 가정하면, 그녀는 두 아들에게 같은 양의 정보를 준 셈이다. 이제 위에서 설명했듯이, 아들들은 각각 부족한 두 자리 숫자를 맞추려고 할 수 있다. 금고를 열려면 각각 최대 100개의 조합만 시도하면 된다.
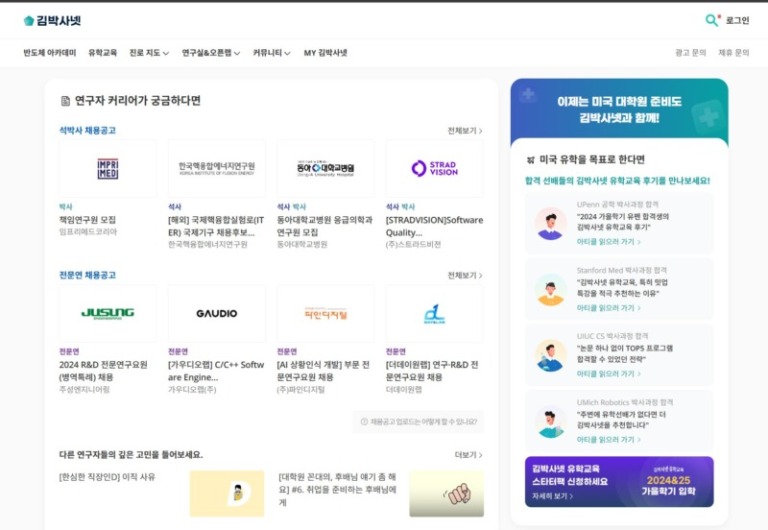
따라서 샤미르는 다른 해결책이 필요했다. 먼저 각 아들이 언뜻 보기에 해답과 전혀 상관없는 정보를 받는 것이 최선일 것이다. 하지만 두 정보를 조합하면 43953이라는 숫자 조합을 쉽게 추론할 수 있어야 하는데, 이를 선형 방정식을 사용하여 우아하고 간단하게 할 방법이 있다. 각 직선은 두 점에 의해 고유하게 정의되는 특성이 있는데, 두 아들에게 직선의 한 점씩의 좌표를 주면 두 아들은 Y축과 교차하는 높이(43953)를 통해 비밀번호를 쉽게 구할 수 있다. 예를 들어, 노파는 직선 y = 5x + 43953의 방정식을 선택해 첫째 아들에게는 점 P1(33503, 211468)의 좌표를, 다른 아들에게는 두 번째 점 P2(85395, 470928)의 좌표를 줄 수 있다. 두 아들이 수학을 잘 못해도 두 점을 평면에 표시하고 자로 연결하여 그 직선이 Y축과 교차하는 지점을 읽으면 금고의 해답을 구할 수 있다. 아들 중 한 명은 한 점만으로는 아무것도 할 수 없다. 한 점을 통과하는 직선은 무한히 많기 때문이다.
만약 이제 이 노파에게 세 아들이 있다면 비슷한 방법으로 방정식을 확장하여 사용할 수 있다. 다만 이 경우 비밀번호를 감추기 위해 직선이 아닌 포물선을 그려야 한다. 노파는 2차 함수 y = 5x2 + 10x + 43953을 선택하여 아들들에게 각각 포물선 상의 점을 줄 수 있다. 이 경우에도 Y축과의 교차점이 원하는 해(43953)에 해당한다. 두 점을 통과하는 포물선은 무한히 존재하기 때문에 두 아들은 세 번째 아들과 협력할 수밖에 없다. 아들이 두 명일 때와 세 명일 때 방정식의 차수 증가할 뿐, 크게 달라지는 부분이 없다. 따라서 노파에게 몇 명의 아들이 있던지 우리는 문제를 일반화할 수 있게 되었다. 따라서 4명의 아들을 둔 노파는 y = ax3 + bx2 + cx + 43953의 방정식으로 풀 수 있다. (이 방정식에서 3이 가장 높은 지수이기 때문에 3차 다항식이라고 한다). 아들이 다섯 명인 노파는 4차 다항식을 사용하면 된다(y = ax4 + bx3 + cx2 + dx + 43953 등). 이 원리는 소위 다항식 보간법에 기초한다. 일반적으로 n차 다항식을 고유하게 결정하려면 n + 1점이 필요하다.
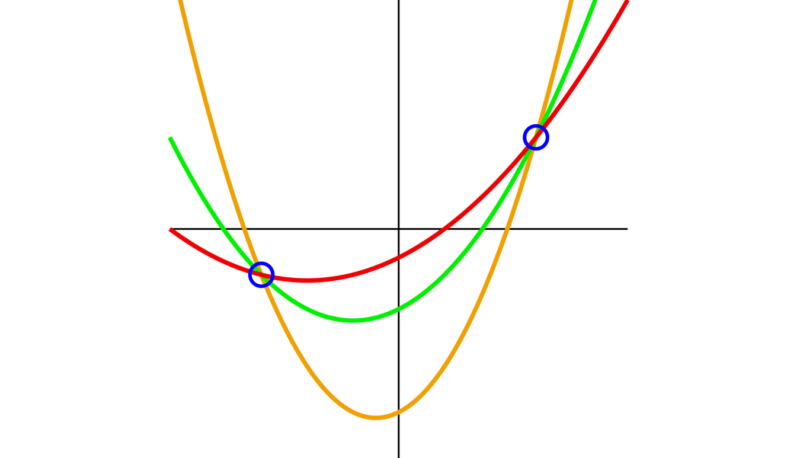
노파는 아들들에게 두 명씩 짝을 지어 금고에 접근하게 할 수도 있다. 이 경우, 금고가 열리려면 5명 중 2명이 있어야 하므로 노파는 다시 직선을 기준으로 선 위에 무작위로 5개의 점을 표시한다. 각 아들에게 좌표를 부여하여 두 아들이 만나면 암호를 해독할 수 있도록 설정할 수 있다. 하지만 여기서 한 가지 함정이 있는데, 5명의 아들 시나리오로 돌아가 보자. 만약 4명이 형제와 공모하면 4점을 이용해 가능한 한 4차 방정식을 풀 수 있다. 물론 암호를 쉽게 구할 수는 없다. 결국 두 개의 미지수, 즉 매개변수 a와 코드 c(이 예시에서는 43953이지만 아들들은 이를 알지 못한다)를 가진 방정식이 남는다. 네 아들은 c가 정수여야 한다는 것을 알고 있다. 또한, 어머니가 곡선상의 점의 좌표를 항상 정수로 주었다면, a도 정수일 것으로 추측할 수 있다. 이것은 가능성의 폭을 상당히 좁혀준다. 형제는 컴퓨터 프로그램을 이용해 다양한 시도로 해답을 찾을 수 있다.
유한체를 적용해 보다 완전한 무작위성을 보장
위의 가능성을 배제하기 위해 샤미르는 또 다른 트릭을 준비했다. 일반적인 실수로 계산하는 대신 더 작은 수 공간, 즉 유한체(finite field)에서 계산하는 것으로 제한한 것이다. 이 숫자 체계에서는 기본적인 사칙연산(덧셈, 곱셈, 뺄셈, 나눗셈)을 정상적으로 수행할 수 있다. 하지만 이 수자 공간에는 무한한 수가 존재하는 것이 아니라 유한한 수만 존재한다.
생소하게 들릴 수도 있지만, 우리는 일상적으로 유한체를 사용하고 있다. 시계만 보더라도 12나 24라는 숫자로 구성되어 있다. 오후 11시에 누군가가 “빵집은 7시간 후에 문을 연다”고 말해도 그것이 6시를 말하는 것임이 모두에게 분명하다. SSS에서도 제한된 수의 범위를 채택하지만, 상한은 대개 큰 소수로 정한다. 이러한 방식으로 숫자 범위가 선택되면 다항식의 그래프는 더 이상 연속곡선이 아니라 평면에 무작위로 분포하는 점에 해당한다.
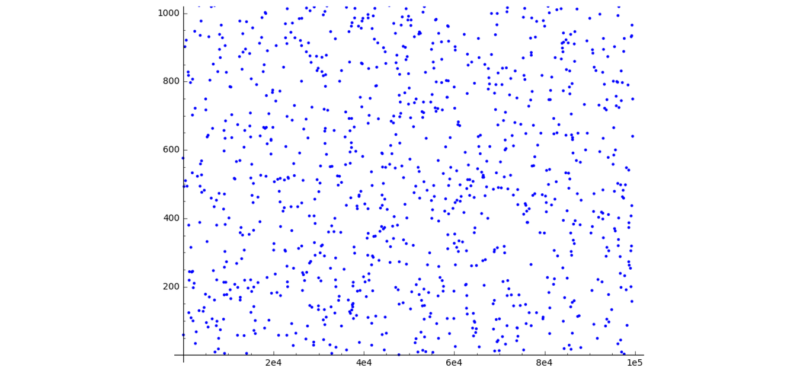
이제 유한체 개념을 통해 형제들이 서로 음모를 꾸미는 것이 사실상 불가능해졌다. 올바른 숫자 코드를 찾기 위해 형제들은 협력해야만 한다. 샤미르의 비밀 공유는 암호화된 이메일 접근을 위한 사용자 키 복구, 암호화폐 지갑에 액세스하는 데 사용되는 마스터 암호를 다시 만드는 데 사용되는 비밀번호를 공유 등에 활용되고 있다.
How Cryptographic ‘Secret Sharing’ Can Keep Information Safe
One safe, five sons and betrayal: this principle shows how shared knowledge can protect secrets—without having to trust anyone
Trust but verify. That expression captures the tension between relying on others while still wanting to keep some level of control over a situation. Mathematician Adi Shamir must have thought about this challenge when he developed what is now known as “Shamir’s secret sharing,” an algorithm named after him.
To understand it, the following puzzle can help: Suppose an elderly woman wants to bequeath the contents of her safe, which is secured with a combination lock, to her five sons, but she is suspicious of each of them. She fears that if she reveals the code to just one, he will make off with the contents. So she wants to give each son a clue such that only the five working together can open the safe. How should the woman proceed?
The task may seem simple. For example, if the combination lock required a five-digit code, she could give each son a number so that they could open it together. But in that scenario, if three sons teamed up, they could likely bypass their two other brothers. Three allies are only two numbers short of the entire code, so they could quickly try out the possible number combinations to get to the coveted contents.
The woman is therefore looking for a way to distribute information that can only be used if all five work together. If two, three or four of the five sons get together, the combined information content must be useless. And that requirement makes the task much more complex.
But in 1979 this challenge did not discourage Shamir. Two years earlier he had developed the so-called “RSA algorithm” together with Ron Rivest and Leonard Adleman. It was the first asymmetric encryption algorithm to be widely adopted, and it is still used today.
SHAMIR’S SECRET SHARING IN ACTION
To understand the Shamir secret-sharing method, it helps to look at a concrete numerical example. Suppose the woman’s secret code is 43953, and, for the sake of simplicity, let’s assume she only has two sons. (We’ll work our way up to the situation with five sons later.)
If the woman were to entrust one son with “439” and the other with “953,” she would have given the two of them the same amount of information. Now, as explained above, the sons could each try to guess the missing two digits. They would only have to try a maximum of 100 combinations each to open the safe.
Shamir therefore needed a different solution. It would be best if each sons received a piece of information that at first glance had nothing to do with the solution. But if you put the two pieces of information together, you should be able to deduce the number combination 43953. And there is an elegant, simple way to do this with the help of a linear equation.
Each straight line is uniquely defined by two points. Shamir realized that the secret number can be encoded in a straight line: for example, as the height at which it intersects the y axis. If you give the two sons the coordinates of one point each on the straight line, they can only determine the number 43953 together. One of the sons cannot do anything with a single point alone: there are an infinite number of straight lines that run through a single point.
The woman could, for example, choose the equation of the line y = 5x + 43953 and give the eldest son the coordinates for a point P1 (33503, 211468) and the other son the coordinates for a second point, P2 (85395, 470928). Even if the two sons are bad at math, they can simply mark the two points in the plane, connect them with a ruler and then read off the point at which the straight line intersects the y axis for the solution to the safe.
So the problem is solved for two sons. If the woman has three sons, she could proceed in a similar way. In this case, however, she would not choose a straight line but rather a parabola to hide the code.
For example, the woman can choose the quadratic function y = 5×2 + 10x + 43953 and give each of her sons a point on the parabola. Again, the point of intersection with the y axis corresponds to the desired solution: 43953. Two of the sons can’t conspire against the third because an infinite number of parabolas can run through two points; the two sons need the help of their brother to find the point of intersection with the y axis and thus the code to the safe.
The principle can be generalized for any number of parties: A woman with four sons can solve an equation of the type y = ax3 + bx2 + cx + 43953. (Because 3 is the highest exponent in this equation, it is called a polynomial equation of the third degree.) A woman with five sons uses a polynomial equation of the fourth degree (such as y = ax4 + bx3 + cx2 + dx + 43953), and so on. The principle is based on so-called polynomial interpolation: in general, n + 1 points are required to uniquely determine a polynomial of the nth degree.
The woman can also give her sons access to the safe in pairs. In this case she relies on the sons controlling each other such that two out of five people need to be present to open the safe. To do this, the woman can again choose a straight line as a base and mark five randomly selected points on it. By giving each son a point, she ensures that two of them can determine the code—regardless of which two of the sons meet.
But there’s a catch. Let’s return to the scenario with the five sons. If four of them conspire against a brother, they can use the four points to solve the fourth-degree equation as far as possible. Of course, they can’t read the code directly from it. In the end they are left with an equation with two unknowns: a parameter a and the code c (which in our example is 43953, but the sons don’t know that).
The four sons know that c must be an integer, however. And if, for example, the woman has always given them integer coordinates for the points on the curve, then they can assume that a probably also has an integer value. This considerably restricts the range of possibilities. The brothers can use a computer program to try out different solutions—and might then determine the correct code.
INTO A DIFFERENT NUMBER RANGE
To avoid such a scenario, Shamir had another trick up his sleeve: instead of calculating with the usual real numbers, he restricted himself to a smaller number space: a finite field. In this number system, the four basic arithmetic operations (addition, multiplication, subtraction and division) can be applied as usual. Instead of an infinite number of numbers, however, this number space only contains a finite number of them.
Though that may sound unfamiliar, we use finite fields every day—for example, whenever we look at the clock. If you only look at the hours, the number range comprises either 12 or 24 numbers. But we still calculate in this limited space: if it’s 11 P.M. and someone says that the bakery opens in seven hours, then it’s clear that they mean six o’clock.
In Shamir’s secret sharing, a restricted number range is also chosen, but the upper limit is usually a large prime number. If the number space is chosen in this way, the graph of a polynomial no longer corresponds to a continuous curve but to randomly distributed points in the plane.
By limiting the woman’s calculations to such a number range, it is practically impossible for the brothers to conspire against each other. To find out the correct numerical code, they have to work together.