Hyoung Keun Kwon (MSc, 2024)
I. 행정구역, 생활구역, 그리고 조세 제도
행정 경계가 겹치는 지역은 복잡한 경제적, 정치적 갈등을 일으킨다. 이러한 상황에서 각 지방 정부는 재원을 유치하려 경쟁하지만, 그 과정에서 예상치 못한 결과와 비효율이 발생할 수 있다.
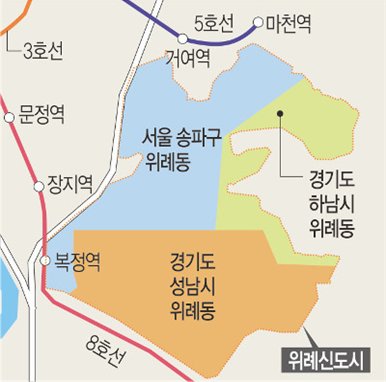
우리나라에서도 새로운 도시 계획을 통해 신도시가 더 생겨나면서 생활권은 같지만 행정구역이 나뉘어 있어 많은 불편이 야기되는 경우가 생긴다. 그러나 단순히 행정구역을 통합한다고 해서 문제가 해결될 것 같지는 않다. 예를 들어, 위례와 강남을 연결하는 문제를 보자. 과연 통합으로 해결될 수 있을까? 문제의 핵심은 ‘재정’에 있다. 중앙 정부, 서울시, 경기도, 하남시, 성남시 등 여러 이해관계가 얽혀 있어 문제는 더욱 복잡하다. 또한, 생활권이 정말로 통합되어 있다고 할 수 있을까? 학군은 물론이고 소방 시설, 동사무소, 도서관 등 편의 시설이 각기 다르게 분포하고 있으며, 이들을 운영하기 위한 재원을 별도로 마련하고 관리하는 것도 큰 과제다.
사실 행정구역 통합 및 편입은 매우 이례적인 일이다. 지자체를 통합 혹은 편입하려는 시도가 여러 번 있었으나 그 수도 적을뿐더러 경남 창원시, 마산시, 진해시가 통합 창원시로, 청주시와 청원군이 통합 청주시가 된 것처럼 시군구 단위의 행정구역 전체가 합쳐지거나 편입이 되었다 (출처: 연합뉴스, 2024). 위례신도시는 하남시, 성남시, 서울시 하의 읍면동 행정구역으로 구성되어 있으며, 상위 행정구역인 하남시, 성남시, 서울시는 각기 다른 입장을 가지고 있다. 신도시 계획 당시 송파신도시라고 불린 것처럼 위례시를 서울 송파구로 편입하려는 시도가 있긴 하지만, 추가적인 행정 및 재정 부담으로 송파구도 쉬이 합병을 원치 않을 것이며, 하남시나 성남시도 세수가 줄어드는 것을 반길 리 없다.
한국 지방 정부의 낮은 재정 자립도
이런 문제가 생긴 근본적인 이유는 지방 정부가 독립적으로 세금을 징수하기 어려워 재정적으로 자립할 수 없다는 점이다. 지방 정부는 세율을 정할 권한이 거의 없으며, 과세 표준(tax base)을 결정할 권한도 없다. 법적으로 탄력세율제도를 통해서 지역자치단체별로 표준세율을 조정할 수 있는 권리를 주었지만, 실제로 활용되는 경우는 거의 없으며 대부분의 지방 정부는 ‘세부담의 형평성’을 고려하여 중앙 정부가 지정한 세율을 그대로 적용한다 (정지선, 2021). 즉, 세율을 조정하는 것이 특별한 이익이나 불이익을 주지 않는 경우에만 법에서 정한 권한을 행사하는 것이다. 지역 간의 균형 발전을 고려해서 재정수요에 비해 수입이 미달하는 금액을 중앙 정부에서 교부금을 통해 교부하지만, 지방 자치 단체에서 주도적으로 수입을 늘리거나 줄일 수는 없다.
미국은 이와 다른 사례를 보여준다. 연방 정부가 최고 권위를 가지고 있지만, 각 주는 자체적으로 세금 종류와 세율을 결정한다. 예를 들어, 추신수 선수가 활동했던 텍사스주는 주 소득세가 없는 반면, 캘리포니아주는 높은 주 소득세율을 적용한다. 델라웨어 주는 판매세(sales tax)가 없는 주로 유명하다. 더 나아가 뉴욕주는 기초 지방 정부(시/타운) 차원에서 부동산을 평가하고 이에 대한 세율을 다르게 부과한다. 뉴욕시는 교통법규에서도 다른 지역과 달리 비보호 우회전을 금지하고, 신호를 기다려 완전히 멈춘 후 우회전을 해야 한다. 물론 미국에서도 연방 혹은 주 정부 차원에서 세금을 걷어 교부금과 같은 방식으로 배분하는 부분도 있지만, 한국에 비해서 지방 정부의 재정 자립도가 높다고 할 수 있다.
미국의 사례에서 보듯이, 각 지방 정부가 독립적으로 세금 정책을 결정할 수 있는 권한은 지방 자치의 자립도를 높이는 중요한 요소다. 그러나 한국은 중앙 정부에 대한 의존도가 높은 만큼 지방 정부가 높은 재정 자립도를 확보하기 어렵다. 특히 위례신도시와 같은 사례에서는, 중앙 정부의 정책, 지방 정부 간의 관계, 그리고 그 정책을 실현하기 위한 재정 마련이 중요한 문제로 대두된다.
조세경쟁 연구의 필요성
위례신도시의 사례로 돌아가 보자. 만약 송파구, 성남시, 하남시가 중앙 정부의 지원만을 기다리지 않고, 자체적으로 재원을 마련할 방법이 있었다면, 위례신사선의 착공 지연 문제를 해결할 수 있었을 것이다. 주민들이 추가로 교통분담금을 납부했음에도 불구하고16년째 공사가 지연되고 있는 현실은, 지방 정부 간의 재정 자립이 얼마나 중요한지를 단적으로 보여준다 (참고: 조선비즈, 2024).
그러나 지방 정부의 조세 권한이 늘어나면 지방 정부 간의 조세경쟁이 불가피하게 대두될 수 있다. 지방 정부가 자율적으로 세율을 조정할 수 있게 되면, 각 지방 정부는 더 많은 자원을 유치하기 위해 경쟁할 수밖에 없다. 이는 지역 간의 조세 정책이 상호 영향을 주고받으며 경쟁하는 양상을 띠게 만들고, 때로는 예상치 못한 결과를 초래할 수 있다. 즉, 세금 경쟁은 지방 정부의 재정 자립도를 높이는 동시에 새로운 도전 과제를 제시할 것이다.
이처럼 정부 정책과 세금 문제는 단순히 중앙과 지방 정부 간의 관계로만 볼 수 없다. 지방 정부 간의 상호작용, 특히 세금 경쟁이 중요한 역할을 하며, 이러한 경쟁이 지역 경제에 미치는 영향은 매우 크다.
연구 핵심 질문
본 연구는 생활권과 조세 관할권이 일치하지 않는 지역에서 발생하는 세금 경쟁을 살펴보고자 한다. 특히 위례신도시와 같이 여러 행정구역이 중첩된 상황에서, 지방정부들이 어떻게 세금 정책을 결정하고 상호작용하는지를 게임 이론적 접근법을 통해 모델을 만들어 경쟁의 특성과 결과를 분석하고자 한다.
구체적으로, 본 연구에서는 다음과 같은 핵심 질문을 다루고자 한다:
- 중첩된 조세 관할권에서 지방정부들은 어떤 전략적 선택을 하는가?
- 이러한 환경에서 세금 경쟁이 전통 모델과 무엇이 다른가?
- 세금 경쟁의 결과로 나타나는 균형 상태는 어떤 특성을 가지는가?
- 이러한 경쟁이 지역 주민의 후생과 공공 서비스 제공에 미치는 영향은 무엇인가?
이러한 분석을 통해, 본 연구는 복잡한 행정 구조를 가진 지역에서 효과적인 재정 정책 수립에 기여하고자 한다. 또한, 위례신도시와 같은 사례에서 나타나는 문제들에 대한 이론적 통찰을 제공하여, 향후 유사한 상황에서 정책 결정에 도움을 줄 수 있을 것으로 예상한다. 다음 장에서는 세금 경쟁에 대해서 보다 구체적으로 다루며 분석을 위한 구체적인 모델과 가정들을 상세히 설명할 예정이다.
II. 조세경쟁 소개
조세경쟁은 지방정부들이 기업과 주민을 유치하기 위해 세율을 낮추는 과정에서 벌어지는 경쟁을 의미한다. 이는 지방 정부의 재정 상황 및 공공서비스 제공에 큰 영향을 미칠 수 있다.
조세경쟁 이론의 기원은 Tiebout(1956)의 “Voting with feet (발에 의한 투표)” 모델로 거슬러 올라간다. Tiebout는 주민들이 자신의 선호에 맞는 세금-공공서비스 조합을 제공하는 지역으로 이동한다고 주장했다. 이후 Oates(1972)는 지방 분권화된 재정 시스템에서 효율적인 공공재 공급이 가능하다고 주장하며, 이를 ‘분권화 정리’로 정립했다.
그러나 Wilson(1986)과 Zodrow and Mieszkowski(1986)는 지방정부 간 조세경쟁이 공공재의 과소공급을 초래할 수 있다고 지적했다. 이들은 자본의 이동성이 높아짐에 따라 지방정부들이 세율을 낮추려는 경향이 있으며, 이는 결과적으로 공공서비스의 질적 저하로 이어질 수 있다고 주장했다.
중첩된 세금 관할권을 가진 지역에서 조세경쟁은 더욱 복잡한 양상을 띤다. Keen and Kotsogiannis(2002)는 수직적 조세경쟁(중앙정부와 지방정부 간)과 수평적 조세경쟁(지방정부들 간)이 동시에 발생하는 상황을 분석했다. 이들은 이러한 중첩된 구조에서 과도한 과세가 발생할 수 있음을 보였다.
위례신도시의 경우, 여러 지방정부의 관할권이 중첩되어 있어 조세경쟁의 양상이 더욱 복잡해진다. 각 정부는 자신의 세수를 극대화하려 하지만, 동시에 다른 정부와의 경쟁도 고려해야 한다. 이는 전통적인 조세경쟁 모델과는 다른 결과를 초래할 수 있다.
정리하면 조세경쟁의 부정적 측면은 다음과 같다:
- 세수입 감소: 세율 인하로 인한 장기적 세수 부족 문제
- 공공서비스 질 저하: 예산 부족으로 인한 서비스 축소
- 지역 간 불균형: 재정 격차로 인한 공공서비스의 지역 간 불균형
- 과도한 재정지출: 기업 유치를 위한 각종 인센티브로 인한 재정 부담
그러나 조세경쟁이 항상 부정적인 것은 아니다. Brennan and Buchanan(1980)은 조세경쟁이 정부의 과도한 팽창을 억제하는 긍정적 역할을 할 수 있다고 주장했다.
중첩된 세금 관할권을 가진 지역에서 조세경쟁 연구는 아직 충분히 이루어지지 않았다. 본 연구는 이러한 상황에서 조세경쟁 양상을 게임 이론적 접근을 통해 분석하고자 한다. 이를 통해 위례신도시와 같은 복잡한 행정 구조를 가진 지역에서 효과적인 재정 정책 수립에 기여할 수 있을 것이다.
III. 게임이론 모델
토이 모델의 필요성
앞서 설명한 복잡한 행정시스템의 모든 세부사항을 고려한 모형을 만들기는 매우 어렵다. 이런 경우 복잡한 많은 디테일을 제거하고 실제 시스템의 핵심적인 부분만 표현한 토이 모델(toy model)이 효과적이다. 예를 들어 자동차가 움직이는 원리를 알고자 엔진 전체를 보면 엔진이 활용하는 연료, 연료 분사 방식, 실린더 배열 방식 등 다양한 요소를 총괄적으로 봐야하므로 복잡하고 쉽게 이해하기 힘들다. 하지만 범퍼카와 같은 토이 모델 자동차를 통해서 악셀을 밟으면 자동차가 앞으로 움직이고 브레이크를 밟으면 정지한다는 원리를 비교적 쉽게 배울 수 있다.
이와 비슷하게 본 연구에서도 세율경쟁의 핵심 메커니즘을 먼저 이해하기 위해서 많은 복잡한 요소를 제거한 토이 모델을 활용할 계획이다. 본 연구를 통해 조세경쟁의 핵심 메커니즘을 이해한 후, 점차 복잡한 요소를 추가하여 추후에는 실제 시스템에 더욱더 가까운 모형을 만드는 것이 목표다.
모델 가정
게임 이론에서 ‘게임’은 여러 플레이어가 각각의 전략을 선택하며 상호작용하는 상황을 의미한다. 각 플레이어는 자신의 목표를 달성하기 위해 최적의 전략을 선택하려고 하며, 이때 다른 플레이어들의 선택도 고려한다.
본 연구에서는 장기 경제 성장을 설명하는 경제 모형인 Solow Model을 활용하여 한 국가 내 두 지역정부의 자본세율 경쟁을 모델링한 Itaya et al. (2008)과 Ogawa and Wang (2016)의 토이 모델에 중첩된 지역을 하나 추가하여 게임을 구성했다. 구체적으로 가상의 국가는 세 개의 지역으로 구성되는데, 두 개 지역은 독립적이고 비대칭적인 자본 요소와 생산기술을 가지며, 세 번째 지역은 다른 두 지역과 동일하게 중첩된다.
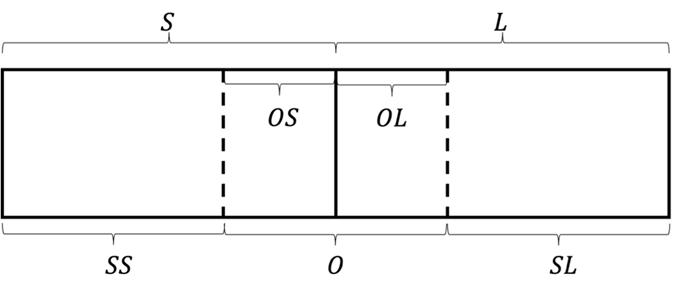
국가 전체 면적을 차지하는 두 개의 독립 지역을 각각 S와 L, 그리고 중첩 지역은 O로 표기하며, 세 지역은 독립적으로 자본세를 부과할 수 있는 권한이 있다고 가정하며 지역 $i$의 세율은 $\tau_i$다. 그리고 S와 L 지역 중 O 지역과 중첩되지 않는 부분을 각각 SS(Sub-S), SL(Sub-L)로 정의하고 S와 O가 중첩되는 지역을 OS, L과 O가 중첩되는 지역을 OL로 표기했다 (그림 2 참조). S와 L은 상위 행정 관할권으로 $G$라는 보편적인 공공재를 제공하며, O는 특수 목적 관할권으로 $H$라는 지역 특수의 공공재를 제공한다.
중첩된 지역의 존재로 ‘자본 세율의 효과’만을 직관적으로 관찰하기 위해서 S와 L 지역의 인구는 동일하다고 가정하며, 가상의 국가에 있는 모든 주민은 동일한 선호 체계를 갖고 각 지역의 회사에 노동력을 비탄성적으로 동일하게 공급하고 있다고 가정한다. 이는 어떤 경우에도 주민들이 이사를 가지 않으며 현재 다니는 회사에서 계속 일을 하는 것이기 때문에 강한 가정이다. 하지만 게임을 그나마 쉽게 풀어내기 위해 필요한 가정이었다. 더 나아가, 각 지역에서 주민들을 고용하고 있는 회사는 동질적인 소비성 제품을 생산한다고 가정했다.
위에서 언급한 것처럼 S와 L은 각각 다른 자본요소와 자본생산기술을 갖고 있다고 가정했다. 이를 수식으로 표현하면 국가 전체의 1인당 평균 자본 부존량 (capital endowment; 원래부터 주어진 자본의 양)은 $\bar{k}$이며, S 와 L지역의 1인당 평균 자본 부존량은 각각
\[ \overline{k_s}\equiv\bar{k}-\varepsilon, \qquad \overline{k_L}\equiv\bar{k}+\varepsilon \qquad where\ \varepsilon\in\left(0,\ \bar{k}\right]\ \ and\ \ \bar{k}\equiv\ \frac{\overline{k_s}+\overline{k_L}}{2} \]
로 표현할 수 있다. 자본 부존량은 다를지 몰라도 같은 국가이기 때문에 자본은 자유롭게 움직일 수 있다. 다시 말하면 S 지역의 주민이 L에 자본을 투자한다고 해서 S지역에 자본을 투자할 때와 비용이 다르지 않다는 것을 의미한다.
몇 개의 필요한 변수들을 간단하게 더 소개하면 지역 $i$에서 요구되는 자본의 양을 $K_i$, 공급되는 노동의 양을 $L_i$, 노동 생산계수와 자본 생산계수는 각각 $A_i$그리고 $B_i > 2K_i$로 정의했다. S와 L지역은 자본생산기술에 차이는 있지만 노동생산기술에는 차이가 없기 때문에 $A_L=A_S$이며 $B_L \neq B_S$이다. O 지역은 가상의 국가에서 새로운 면적을 차지하는 것이 아닌 S와 L 지역을 면적, 인구 관점에서 동일한 비율로 중첩된 상태이기 때문에 $A_O=A_L=A_S$이며 $B_O$는 $B_L$과 $B_S$의 가중치가 각각 OL과 OS지역에 투자된 자본의 비율인 가중 평균 값일 것이다.
시장 균형
위에 소개한 변수들을 활용하여 본 연구에서 활용하는 지역 $i$의 규모수익불변 (CRS; Constant Returns to Scale) 1 생산 함수를 표현하면 다음과 같다.
\[ F_i\left(L_i,\ K_i\right)=A_iL_i+B_iK_i-\frac{K_i^2}{L_i} \]
위 생산 함수를 기반으로 기업은 이윤을 극대화한다고 가정하며, 전체 자본 부존도와 자본 투자수요가 동일할 때 시장 균형이 이루어진다고 가정한다. 이를 기반으로 시장 균형에서의 자본 수요와 이자를 계산하면
\[
\begin{align*}
r^* &= \frac{1}{2}\left(\left(B_S+B_L\right)-\left(\tau_S+\tau_L+\left(2-\alpha_S-\alpha_L\right)\tau_O\right)\right)-2\bar{k} \\
K_S^* &= l\left(\bar{k}+\frac{1}{4}\left(\left(\tau_L-\tau_S-\left(\alpha_L-\alpha_S\right)\tau_O\right)-\left(B_L-B_S\right)\right)\right) \\
K_L^* &= l\left(\bar{k}+\frac{1}{4}\left(\left(\tau_S-\tau_L+\left(\alpha_L-\alpha_S\right)\tau_O\right)+\left(B_L-B_S\right)\right)\right) \\
K_{SS}^* &= \frac{2l}{3}\left(\bar{k}+\frac{1}{4}\left(\left(\tau_L-\tau_S+\left(2-\alpha_L-\alpha_S\right)\tau_O\right)-\left(B_L-B_S\right)\right)\right) \\
K_{SL}^* &= \frac{2l}{3}\left(\bar{k}+\frac{1}{4}\left(\left(\tau_S-\tau_L+\left(2-\alpha_L-\alpha_S\right)\tau_O\right)+\left(B_L-B_S\right)\right)\right) \\
K_O^* &= \frac{2l}{3}\left(\bar{k}-\frac{1}{2}\left(2-\alpha_L-\alpha_S\right)\tau_O\right)
\end{align*}
\]
로 정리되며, 여기서 $K_{SS}=\alpha_S K_S$, $K_{SL}=\alpha_L K_L$이며 $0<\alpha_S, \alpha_L < 1$이다. 또한, $B_L-B_S=\theta$로 정의하겠다.
주민들은 세후 소득을 극대화하기 위해 자본 투자를 하며 시장 균형 상의 자본 수익 $r^*$의 소득을 얻고 이를 모두 소비한다. 조세 관할권에서는 세금을 통해 각각의 공공재를 제공하며, 개인의 소비, 공공재 제공량의 합으로 표현되는 다음의 사회 효용 함수를 극대화하기 위한 자본세율 $\tau_i^*$를 선택한다고 가정한다.
$ u \left( C_i, G_i, H_i \right) \equiv C_i + G_i + H_i = $
\[
\begin{cases}
l\left( w_i^* + r^* \bar{k}_i \right) + K_i^* \tau_i + (1 – \alpha_i) K_i^* \tau_O, & \text{for } i \in {S, L} \\
\dfrac{2l}{3}\left( w_O^* + r^* \bar{k} \right) + K_O^* \tau_O + (1 – \alpha_S) K_S^* \tau_S + (1 – \alpha_L) K_L^* \tau_L, & \text{for } i = O
\end{cases}
\]
그러면 시장 균형에서의 세율은
\[
\begin{align*}
\tau_S^\ast &= \frac{4\varepsilon}{3}-\frac{\theta}{3}+\frac{\tau_L}{3}-\frac{2-3\alpha_S+\alpha_L}{3}\tau_O \\
\tau_L^\ast &= -\frac{4\varepsilon}{3}+\frac{\theta}{3}+\frac{\tau_S}{3}-\frac{2-3\alpha_L+\alpha_S}{3}\tau_O \\
\tau_O^\ast &= \frac{3\left(\alpha_L+\alpha_S\right)-4}{\left(2-\left(\alpha_L+\alpha_S\right)\right)\left(\alpha_L+\alpha_S\right)}\bar{k}=\Gamma\bar{k}
\end{align*}
\]
IV. 내쉬 균형 및 시뮬레이션 결과
내쉬 균형
먼저 내쉬 균형(Nash Equilibrium)에 대해 간단히 설명하면, 게임에 참여한 모든 플레이어가 최선의 선택을 하고 더 이상 자신의 전략을 바꿀 유인이 없는 상태를 말한다. 다시 말하면, 내쉬 균형에서는 자신의 전략을 바꿔서 이익을 얻을 수 있는 플레이어가 없으므로 모든 플레이어가 현재의 전략을 유지한다.
앞 장에서 계산한 시장 균형에서의 세율은 각 지역에서 선택할 수 있는 최적 반응 함수라고 표현할 수 있다. 다른 지역의 전략이 주어졌을 때 사회 효용 함수를 극대화할 수 있는 최적의 전략이기 때문이다. 다시 말해, 지역 $i$가 다른 지역의 세율에 대해 어떤 세율을 선택하는 것이 가장 유리한지 보여주는 함수다. 그렇기 때문에 시장 균형에서의 세율을 기반으로 내쉬 균형 세율을 구할 수 있으며, 다음과 같은 식으로 표현할 수 있다.
\[
\begin{align*}
\tau_S^N &= \varepsilon-\frac{\theta}{4}-\Gamma\left(1-\alpha_S\right)\bar{k} \\
\tau_L^N &= -\left(\varepsilon+\frac{\theta}{4}\right)-\Gamma\left(1-\alpha_L\right)\bar{k} \\
\tau_O^N &= \Gamma\bar{k}
\end{align*}
\]
위 내용을 토대로 부명제(Lemma)와 명제(Proposition)를 도출할 수 있다.
Lemma 1. $\Phi\equiv\varepsilon-\frac{\theta}{4}$가 S와 L 지역의 순자본위치(Net Capital Position)를 결정한다. $\Phi$가 0보다 클 때 L이 순자본을 수출하며 S가 순자본을 수입한다. 0보다 작을 때는 L이 순자본을 수입하며 L이 순자본을 수출한다.
Proposition 1. $\Gamma\equiv\frac{3\left(\alpha_L+\alpha_S\right)-4}{\left(2-\left(\alpha_L+\alpha_S\right)\right)\left(\alpha_L+\alpha_S\right)}$의 부호가 O 지역의 실질적 세율의 부호를 결정하며, $\alpha_L+\alpha_S$가 4/3보다 커야 양(+)의 $H$를 제공할 수 있다.
그리고 내쉬 균형에서 자본 수요와 이자는 다음과 같다.
\[
\begin{align*}
r^N&=\frac{1}{2\left(B_S+B_L\right)}-2\bar{k} \\
K_S^N&=l\left({\bar{k}}_S+\frac{1}{2}\left(\varepsilon-\frac{\theta}{4}\right)\right) \\
K_L^N&=l\left({\bar{k}}_L-\frac{1}{2}\left(\varepsilon-\frac{\theta}{4}\right)\right) \\
K_{SS}^N&=\frac{2l}{3}\left({\bar{k}}_S+\frac{1}{2}\bar{k}\Gamma\left(1-\alpha_S\right)-\frac{1}{2}\left(\varepsilon+\frac{\theta}{4}\right)\right) \\
K_{SL}^N&=\frac{2l}{3}\left({\bar{k}}_L+\frac{1}{2}\bar{k}\Gamma\left(1-\alpha_L\right)+\frac{1}{2}\left(\varepsilon+\frac{\theta}{4}\right)\right) \\
K_O^N&=\frac{l}{3}\cdot\frac{4-\alpha_L-\alpha_S }{\alpha_L+\alpha_S}\bar{k}
\end{align*}
\]
시뮬레이션을 통한 시각화
위 내쉬 균형은 비선형(nonlinear)이기 때문에 시뮬레이션을 통해 결과를 시각화 할 수 있다. $\alpha_S$, $\alpha_L$, $\epsilon$, $\theta$를 조절하여 시뮬레이션하면 부명제 1에서 언급한 것처럼 $\Phi$가 0 보다 크면 L 지역의 자본수요가 줄어들고 S 지역의 자본수요가 늘어나면서 L 이 자본을 수출하고 S가 자본을 수입하게 된다 (그림 3 참조).
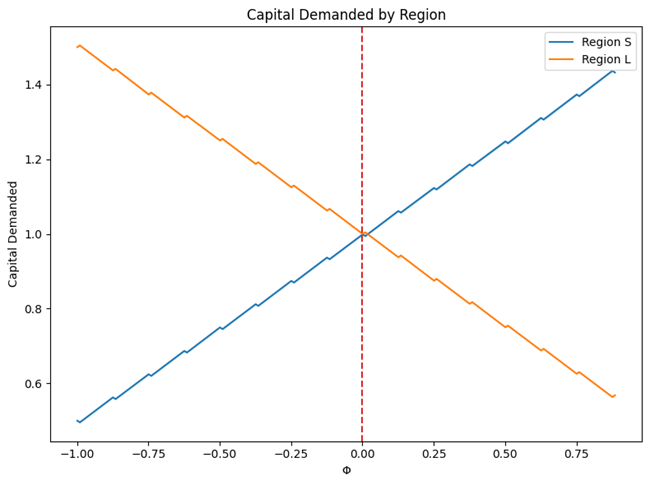
그리고 내쉬 균형 결과를 기반으로 각 지역의 대표 주민이 공공재로부터 얻는 효용은 다음과 같이 정리할 수 있는데,
\[
u_p(G_i, H_i) =
\begin{cases}
\frac{K_S^N \tau_S}{l} & \text{for } i = SS \\
\frac{K_L^N \tau_L}{l} & \text{for } i = SL \\
\frac{K_S^N \tau_S}{l} + \frac{3 K_O^* \tau_O }{2l} & \text{for } i = OS \\
\frac{K_L^N \tau_L}{l} + \frac{3 K_O^* \tau_O }{2l} & \text{for } i = OL
\end{cases}
\]
이를 시뮬레이션하여 시각화하면 (그림 4)가 된다.
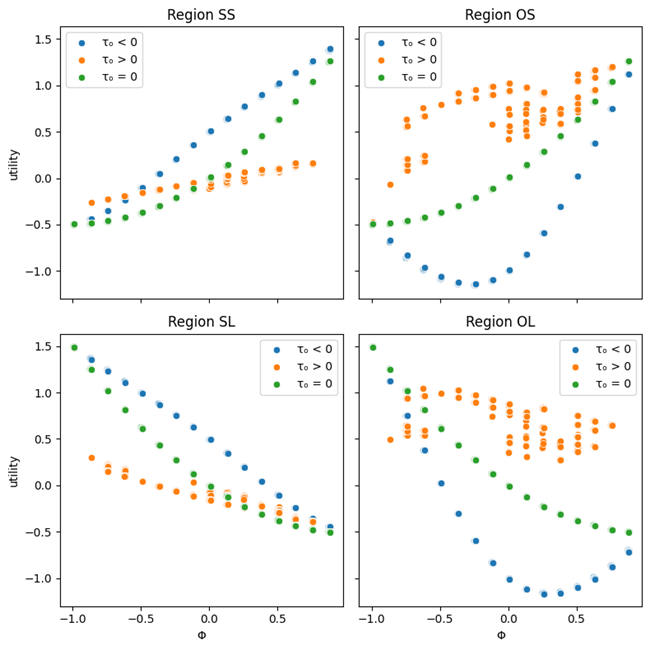
위 내용을 정리하면 지역 O의 경우, S와 L의 세율로부터 직접적인 영향을 받지 않고 배분된 자원의 비율, 즉 $\alpha_S$와 $\alpha_L$의 합에 직접적으로 영향을 받는다. S 와 L 은 O 라는 특수 목적 관할권의 존재로 특수 목적 관할권이 없을 때에 비해 각각 $\Gamma\left(1-\alpha_S\right)\bar{k}$그리고 $\Gamma\left(1-\alpha_L\right)\bar{k}$만큼 세율이 변한다. 그리고 순자본위치는 특수 목적 관할권과는 무관하게 정해진다는 것을 알 수 있다.
V. 결론 및 함의
본 연구는 중첩된 세금 관할권을 가진 지역에서 조세경쟁이 어떻게 전개되는지를 게임 이론적 접근을 통해 살펴봤다. 특히, 위례신도시와 같은 복잡한 행정 구조에서 조세경쟁이 미치는 영향을 이해하기 위해 단순화된 토이 모델을 구축하고, 이를 기반으로 내쉬 균형을 도출했다. 이를 통해 중첩된 조세 관할권이 존재할 때, 조세경쟁의 양상과 그 결과가 Itaya et al. (2008)과 Ogawa and Wang (2016)의 모델에서 예측되는 것과 다른 부분이 있음을 확인했다.
그러나 이 연구는 여러 한계를 가지고 있다. 첫째, 토이 모델을 사용해 현실의 복잡한 세부 사항을 단순화했기 때문에, 실제 상황에서 나타날 수 있는 다양한 요인을 충분히 반영하지 못했다. 예를 들어, 인구 이동성, 정부의 정책적 대응, 다양한 과세 표준, 그리고 주민들 간의 소득 격차와 같은 요소들이 모델에서 제외되었으며, 이는 결과의 일반화 가능성을 제한한다. 둘째, 모델에서 가정한 경제적 변수들, 예를 들어 자본 부존량과 생산기술의 차이, 공공재에 대한 주민의 선호 등이 실제와 다를 수 있어, 이를 현실에 적용하는 데에는 신중한 접근이 필요하다.
이러한 한계에도 불구하고, 본 연구는 중첩된 행정 구조에서 조세경쟁의 동태를 이해하는 데 중요한 이론적 기초를 제공한다. 특히, 단순한 세율 인하 경쟁을 넘어서, 지역 간 자본 이동과 공공재 제공의 상호작용을 고려한 정책적 접근이 필요함을 시사한다.
향후 연구에서는 이 연구의 모델을 더욱 확장하여, 인구 이동성, 정부의 정책적 대응과 같은 추가적인 변수들을 포함할 필요가 있다. 더 나아가 게임이 반복해서 진행될 때는 어떻게 세율 경쟁이 진행되는지 볼 필요가 있다. 마지막으로는 다양한 경제적, 사회적 조건 하에서 모델을 테스트함으로써, 실제 정책 적용에 대한 신뢰성을 높이는 작업이 이루어져야 할 것이다. 이를 통해 복잡한 행정 구조 속에서 조세경쟁의 실질적 영향을 보다 정확하게 파악하고, 효과적인 정책을 설계하는 데 기여할 수 있을 것이다.
VI. 참고 문헌
정지선. (2021). 탄력세율제도의 개선방안에 대한 연구. 한국지방세연구원.
Brennan, G., & Buchanan, J. M. (1980). The power to tax: Analytical foundations of a fiscal constitution. Cambridge University Press.
Keen, M., & Kotsogiannis, C. (2002). Does federalism lead to excessively high taxes? American Economic Review, 92(1), 363-370.
Itaya, J.-i., Okamura, M., & Yamaguchi, C. (2008). Are regional asymmetries detrimental to tax coordination in a repeated game setting? Journal of Public Economics, 92(12), 2403–2411.
Oates, W. E. (1972). Fiscal federalism. Harcourt Brace Jovanovich.
Ogawa, H., & Wang, W. (2016). Asymmetric tax competition and fiscal equalization in a repeated game setting. International Review of Economics & Finance, 41, 1–10.
Tiebout, C. M. (1956). A pure theory of local expenditures. Journal of Political Economy, 64(5), 416-424.
Wilson, J. D. (1986). A theory of interregional tax competition. Journal of Urban Economics, 19(3), 296-315.
Zodrow, G. R., & Mieszkowski, P. (1986). Pigou, Tiebout, property taxation, and the underprovision of local public goods. Journal of Urban Economics, 19(3), 356-370.
- 규모수익불변 생산함수란, 투입량의 증가율과 산출량의 증가율이 동일한 함수이다. 예를 들어 투입된 노동과 자본의 양이 각각 2배 늘어나면 산출량 역시 2배 늘어난다는 의미다. [↩]
























